题目内容
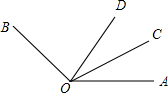 如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.考点:角平分线的定义
专题:
分析:用∠AOC表示出∠AOB的度数,再根据角平分线的定义得出∠AOD的度数,根据∠COD=∠AOD-∠AOC即可得出结论.
解答:解:∵∠BOC=2∠AOC,
∴∠AOB=∠BOC+∠AOC=3∠AOC.
∵OD平分∠AOB,
∴∠AOD=
∠AOB=
∠AOC,
∵∠COD=25°,
∴∠COD=∠AOD-∠AOC=
∠AOC-∠AOC=
∠AOC=25°,解得∠AOC=50°.
∴∠AOB=∠BOC+∠AOC=3∠AOC.
∵OD平分∠AOB,
∴∠AOD=
| 1 |
| 2 |
| 3 |
| 2 |
∵∠COD=25°,
∴∠COD=∠AOD-∠AOC=
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
相关题目
已知圆的半径是R,则圆内接正十边形的边长是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 如图,抛物线y=-
如图,抛物线y=- 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,解这个直角三角形.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,解这个直角三角形. 如图,BD、CE相交于点A.
如图,BD、CE相交于点A.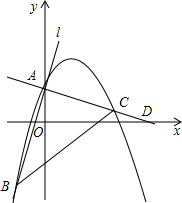 如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(-2,-4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(-2,-4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D. 为测量学校操场上旗杆的高度,某数学活动小组设计如下测量方法:将镜子放在离旗杆(AB)27m的点E处,然后沿直线BE后退,使在点D处恰好看到旗杆顶端A在镜子中的像与镜子上的标记重合(如图),若DE=2.4m,观测者的眼睛离地面的高度CD为1.6m,求旗杆的高度.
为测量学校操场上旗杆的高度,某数学活动小组设计如下测量方法:将镜子放在离旗杆(AB)27m的点E处,然后沿直线BE后退,使在点D处恰好看到旗杆顶端A在镜子中的像与镜子上的标记重合(如图),若DE=2.4m,观测者的眼睛离地面的高度CD为1.6m,求旗杆的高度.