题目内容
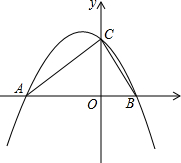 如图,抛物线y=-
如图,抛物线y=-| 3 |
| 8 |
| 3 |
| 4 |
(1)求点A,B的坐标;
(2)∠ACB是直角吗?写出你的判断理由;
(3)以AB为直径的圆与y轴负半轴交于点E,求过A,E,B三点的抛物线的解析式.
考点:二次函数综合题
专题:
分析:(1)令y=0,求出x的值,即可得出点A,B的坐标;
(2)分别求出AC、BC、AB的长度,判断是否符合勾股定理,即可判断∠ACB是否为直角;
(3)根据题意作出圆,求出点E的坐标,运用待定系数法求出过A,E,B三点的抛物线的解析式.
(2)分别求出AC、BC、AB的长度,判断是否符合勾股定理,即可判断∠ACB是否为直角;
(3)根据题意作出圆,求出点E的坐标,运用待定系数法求出过A,E,B三点的抛物线的解析式.
解答:解:(1)令y=0,
则-
x2-
x+3=0,
解得:x1=-2,x2=4,
即点A,B的坐标分别为(-2,0),(4,0);
(2)令x=0,
解得:y=3,
即点C(0,3),
则OC=3,
∵OA=4,OB=2,
∴AC=
=5,BC=
=
,
∴AC2+BC2=25+13=38,
∵AB2=62=36≠AC2+BC2,
∴∠ACB不是直角;
(3)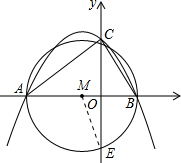 由题意得,M(-1,0),ME=3,
由题意得,M(-1,0),ME=3,
则OE=
=2
,
即点E(0,-2
),
设过A,E,B三点的抛物线的解析式为y=ax2+bx+c,
则有
,
解得:
,
即过A,E,B三点的抛物线的解析式为:y=
x2+
x-2
.
则-
| 3 |
| 8 |
| 3 |
| 4 |
解得:x1=-2,x2=4,
即点A,B的坐标分别为(-2,0),(4,0);
(2)令x=0,
解得:y=3,
即点C(0,3),
则OC=3,
∵OA=4,OB=2,
∴AC=
| OA2+OC2 |
| OC2+OB2 |
| 13 |
∴AC2+BC2=25+13=38,
∵AB2=62=36≠AC2+BC2,
∴∠ACB不是直角;
(3)
 由题意得,M(-1,0),ME=3,
由题意得,M(-1,0),ME=3,则OE=
| ME2-OM2 |
| 2 |
即点E(0,-2
| 2 |
设过A,E,B三点的抛物线的解析式为y=ax2+bx+c,
则有
|
解得:
|
即过A,E,B三点的抛物线的解析式为:y=
| ||
| 4 |
| ||
| 2 |
| 2 |
点评:本题考查了二次函数的综合应用,涉及了勾股定理、待定系数法求函数解析式等知识,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
反比例函数y=
的图象在第一、三象限,则m的取值范围是( )
| m-1 |
| x |
| A、m≥1 | B、m≤1 |
| C、m>1 | D、m<1 |
下列说法正确的是( )
| A、-2不是单项式 | ||
| B、-a表示负数 | ||
C、
| ||
D、
|
方程x2=2x的解是( )
| A、x=0 | ||
| B、x=2 | ||
| C、x1=0 x2=2 | ||
D、x1=0 x2=
|
下列各对数中互为倒数的是( )
| A、5和-5 | ||
B、-3和
| ||
C、-2和-
| ||
| D、0和0 |
 如图,抛物线y=ax2+bx+c与坐标轴分别交于A(-3,0),B(1,0),C(0,3),D是抛物线顶点,E是对称轴与x轴的交点
如图,抛物线y=ax2+bx+c与坐标轴分别交于A(-3,0),B(1,0),C(0,3),D是抛物线顶点,E是对称轴与x轴的交点 如图所示,Rt△ABC,AB=2,AC=1,∠B=30°.请你添加你喜欢的辅助线,求出tan15°的值.
如图所示,Rt△ABC,AB=2,AC=1,∠B=30°.请你添加你喜欢的辅助线,求出tan15°的值. 如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数. 如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.
如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.