题目内容
已知圆的半径是R,则圆内接正十边形的边长是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正多边形和圆
专题:
分析:设AB是圆内接正十边形的边长,连接OA、OB,作∠OAB的平分线交OB于C,求出∠O=∠CAB,OC=AC=AB,证△OAB∽△ACB,得出比例式,即可求出答案.
解答:解:设AB是圆内接正十边形的边长,
 连接OA、OB,作∠OAB的平分线交OB于C,
连接OA、OB,作∠OAB的平分线交OB于C,
则∠AOB=
=36°,
∠OAB=∠OBA=72°,∠OAC=∠BAC=36°,
所以∠ACB=36°+36°=72°,
∵∠B=72°,
∴∠ACB=∠B,
∴AC=AB,AC=OC,
∵∠O=∠CAB=36°,∠B=∠B,
∴△OAB∽△ACB,
∴
=
,
∵OA=OB=R,
∴
=
,
解得:AB=
R.
故选B.
 连接OA、OB,作∠OAB的平分线交OB于C,
连接OA、OB,作∠OAB的平分线交OB于C,则∠AOB=
| 360° |
| 10 |
∠OAB=∠OBA=72°,∠OAC=∠BAC=36°,
所以∠ACB=36°+36°=72°,
∵∠B=72°,
∴∠ACB=∠B,
∴AC=AB,AC=OC,
∵∠O=∠CAB=36°,∠B=∠B,
∴△OAB∽△ACB,
∴
| OA |
| AC |
| AB |
| BC |
∵OA=OB=R,
∴
| R |
| AB |
| AB |
| R-AB |
解得:AB=
| ||
| 2 |
故选B.
点评:本题考查了正多边形和圆,等腰三角形的判定,相似三角形的性质和判定的应用,解此题的关键是得出关于AB的比例式,题目是一道比较好的题目,难度适中.

练习册系列答案
相关题目
下列说法正确的是( )
| A、-2不是单项式 | ||
| B、-a表示负数 | ||
C、
| ||
D、
|
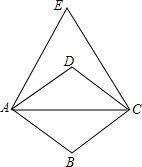 如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )
如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )| A、25° | B、35° |
| C、45° | D、55° |
 如图所示,Rt△ABC,AB=2,AC=1,∠B=30°.请你添加你喜欢的辅助线,求出tan15°的值.
如图所示,Rt△ABC,AB=2,AC=1,∠B=30°.请你添加你喜欢的辅助线,求出tan15°的值.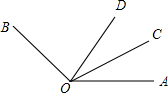 如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.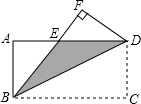 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB= 如图,等腰△OAB,OA=OB,以O为圆心画圆,与AB、OA、OB分别交于点C、D、E、F,求证:
如图,等腰△OAB,OA=OB,以O为圆心画圆,与AB、OA、OB分别交于点C、D、E、F,求证:
 如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.
如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.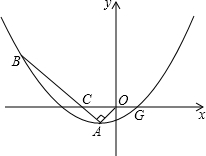 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).