题目内容
图1和图2,半圆O的直径AB=2,点P(不与点A,B重合)为半圆上一点,将图形延BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.
(1)当α=15°时,过点A′作A′C∥AB,如图1,判断A′C与半圆O的位置关系,并说明理由.
(2)如图2,当α= °时,BA′与半圆O相切.当α= °时,点O′落在
上.
(3)当线段BO′与半圆O只有一个公共点B时,求α的取值范围.
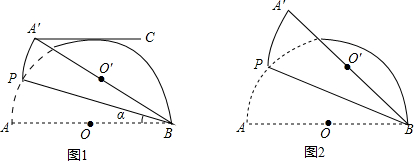
(1)当α=15°时,过点A′作A′C∥AB,如图1,判断A′C与半圆O的位置关系,并说明理由.
(2)如图2,当α=
 |
| PB |
(3)当线段BO′与半圆O只有一个公共点B时,求α的取值范围.

考点:圆的综合题
专题:
分析:(1)过O作OD⊥A′C于点D,交A′B于点E,利用含30°角的直角三角形的性质可求得DE+OE=
A′B=
AB=OA,可判定A′C与半圆相切;
(2)当BA′与半圆相切时,可知OB⊥A′B,则可知α=45°,当O′在
上时,连接AO′,则可知BO′=
AB,可求得∠O′BA=60°,可求得α=30°;
(3)利用(2)可知当α=30°时,线段O′B与圆交于O′,当α=45°时交于点B,结合题意可得出满足条件的α的范围.
| 1 |
| 2 |
| 1 |
| 2 |
(2)当BA′与半圆相切时,可知OB⊥A′B,则可知α=45°,当O′在
 |
| PB |
| 1 |
| 2 |
(3)利用(2)可知当α=30°时,线段O′B与圆交于O′,当α=45°时交于点B,结合题意可得出满足条件的α的范围.
解答:解:(1)相切,理由如下:
如图1,过O作OD过O作OD⊥A′C于点D,交A′B于点E,

∵α=15°,A′C∥AB,
∴∠ABA′=∠CA′B=30°,
∴DE=
A′E,OE=
BE,
∴DO=DE+OE=
(A′E+BE)=
AB=OA,
∴A′C与半圆O相切;
(2)当BA′与半圆O相切时,则OB⊥BA′,
∴∠OBA′=2α=90°,
∴α=45°,
当O′在
上时,如图2,

连接AO′,则可知BO′=
AB,
∴∠O′AB=30°,
∴∠ABO′=60°,
∴α=30°,
故答案为:45;30;
(3)∵点P,A不重合,∴α>0,
由(2)可知当α增大到30°时,点O′在半圆上,
∴当0°<α<30°时点O′在半圆内,线段BO′与半圆只有一个公共点B;
当α增大到45°时BA′与半圆相切,即线段BO′与半圆只有一个公共点B.
当α继续增大时,点P逐渐靠近点B,但是点P,B不重合,
∴α<90°,
∴当45°≤α<90°线段BO′与半圆只有一个公共点B.
综上所述0°<α<30°或45°≤α<90°.
如图1,过O作OD过O作OD⊥A′C于点D,交A′B于点E,

∵α=15°,A′C∥AB,
∴∠ABA′=∠CA′B=30°,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DO=DE+OE=
| 1 |
| 2 |
| 1 |
| 2 |
∴A′C与半圆O相切;
(2)当BA′与半圆O相切时,则OB⊥BA′,
∴∠OBA′=2α=90°,
∴α=45°,
当O′在
 |
| PB |

连接AO′,则可知BO′=
| 1 |
| 2 |
∴∠O′AB=30°,
∴∠ABO′=60°,
∴α=30°,
故答案为:45;30;
(3)∵点P,A不重合,∴α>0,
由(2)可知当α增大到30°时,点O′在半圆上,
∴当0°<α<30°时点O′在半圆内,线段BO′与半圆只有一个公共点B;
当α增大到45°时BA′与半圆相切,即线段BO′与半圆只有一个公共点B.
当α继续增大时,点P逐渐靠近点B,但是点P,B不重合,
∴α<90°,
∴当45°≤α<90°线段BO′与半圆只有一个公共点B.
综上所述0°<α<30°或45°≤α<90°.
点评:本题主要考查切线的判定和性质及含特殊角的直角三角形的性质,掌握切线的判定和性质是解题的关键,注意切线的判定方法有两种,即①有切点时连接圆心和切点证明垂直,②无切点时作垂直证明圆心到直线的距离等于半径;在(3)中注意结合(2)的两个极端情况进行判断范围即可.本题难度适中,属于综合性的基础题目.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
反比例函数y=
的图象在第一、三象限,则m的取值范围是( )
| m-1 |
| x |
| A、m≥1 | B、m≤1 |
| C、m>1 | D、m<1 |
下列四个算式中,正确的是( )
| A、a3•a2=2a6 |
| B、b3+b3=b6 |
| C、x•x4=x4 |
| D、y5+y5=2y5 |
下列运算正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知两圆的半径分别为7和1,当它们内切时,圆心距为( )
| A、6 | B、7 | C、8 | D、9 |
下列说法正确的是( )
| A、-2不是单项式 | ||
| B、-a表示负数 | ||
C、
| ||
D、
|
方程x2=2x的解是( )
| A、x=0 | ||
| B、x=2 | ||
| C、x1=0 x2=2 | ||
D、x1=0 x2=
|
 如图,是由一个长方体和一个圆锥体组成的立体图形,从正面看得到的平面图形是( )
如图,是由一个长方体和一个圆锥体组成的立体图形,从正面看得到的平面图形是( )



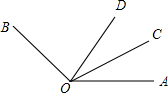 如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.