题目内容
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,解这个直角三角形.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,解这个直角三角形.考点:解直角三角形
专题:
分析:首先求出AB的长度;运用勾股定理求出BC的长度,即可解决问题.
解答: 解:∵∠C=90°,∠B=30°,AC=6,
解:∵∠C=90°,∠B=30°,AC=6,
∴AB=2AC=12,∠A=90°-60°=30°;
由勾股定理得:BC2=AB2-AC2,
∴BC=6
;
即AB=12,BC=6
,∠A=60°.
 解:∵∠C=90°,∠B=30°,AC=6,
解:∵∠C=90°,∠B=30°,AC=6,∴AB=2AC=12,∠A=90°-60°=30°;
由勾股定理得:BC2=AB2-AC2,
∴BC=6
| 3 |
即AB=12,BC=6
| 3 |
点评:该题主要考查了直角三角形的边角关系及其应用问题;牢固掌握勾股定理、直角三角形的边角关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列四个算式中,正确的是( )
| A、a3•a2=2a6 |
| B、b3+b3=b6 |
| C、x•x4=x4 |
| D、y5+y5=2y5 |
方程x2=2x的解是( )
| A、x=0 | ||
| B、x=2 | ||
| C、x1=0 x2=2 | ||
D、x1=0 x2=
|
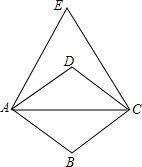 如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )
如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )| A、25° | B、35° |
| C、45° | D、55° |
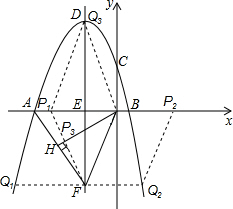 如图,抛物线y=ax2+bx+c与坐标轴分别交于A(-3,0),B(1,0),C(0,3),D是抛物线顶点,E是对称轴与x轴的交点
如图,抛物线y=ax2+bx+c与坐标轴分别交于A(-3,0),B(1,0),C(0,3),D是抛物线顶点,E是对称轴与x轴的交点 如图所示,Rt△ABC,AB=2,AC=1,∠B=30°.请你添加你喜欢的辅助线,求出tan15°的值.
如图所示,Rt△ABC,AB=2,AC=1,∠B=30°.请你添加你喜欢的辅助线,求出tan15°的值.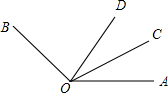 如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,∠COD=25°,求∠AOC的度数.