题目内容
 如图所示,在△ABC中,P是BC边上的一点,试说明AB2•PC+AC2•PB=BC(AP2+PB•PC).
如图所示,在△ABC中,P是BC边上的一点,试说明AB2•PC+AC2•PB=BC(AP2+PB•PC).考点:勾股定理
专题:证明题
分析:过A作AD⊥BC于D.根据勾股定理可得AB2×PC+AC2×PB=BC×AD2+BD2×PC+CD2×PB,不妨设D在P右边(左边同理可证),得到BD2×PC+CD2×PB=BC×(BP×CP+DP2),AB2×PC+AC2×PB=BC×(AP2+PB×PC),依此即可求解.
解答: 证明:过A作AD⊥BC于D.
证明:过A作AD⊥BC于D.
∵AD⊥BC,
∴AB2=AD2+BD2,AC2=AD2+CD2,
∴AB2×PC+AC2×PB
=(AD2+BD2)×PC+(AD2+CD2)×PB
=AD2(PB+PC)+BD2×PC+CD2×PB
=BC×AD2+BD2×PC+CD2×PB,
不妨设D在P右边(左边同理可证),
BD2×PC+CD2×PB
=BD2×(CD+PD)+CD2×(BD-DP)
=BD2×CD+CD2×BD+PD(BD2-CD2)
=BD×CD×(BD+CD)+PD×(BD+CD)×(BD-CD)
=BD×CD×BC+DP×BC×(BD-CD)
=BC×(BD×CD-DP×CD+DP×BD)
=BC×(BP×CD+DP×BD)
=BC×(BP×CD+DP×BP+DP×DP)
=BC×(BP×CP+DP2),
∴AB2×PC+AC2×PB
=BC×AD2+BD2×PC+CD2×PB
=BC×AD2+BC×(BP×CP+DP2)
=BC×(AD2+DP2+BP×CP)
=BC×(AP2+PB×PC),
即AB2×PC+AC2×PB=BC×(AP2+PB×PC).
 证明:过A作AD⊥BC于D.
证明:过A作AD⊥BC于D.∵AD⊥BC,
∴AB2=AD2+BD2,AC2=AD2+CD2,
∴AB2×PC+AC2×PB
=(AD2+BD2)×PC+(AD2+CD2)×PB
=AD2(PB+PC)+BD2×PC+CD2×PB
=BC×AD2+BD2×PC+CD2×PB,
不妨设D在P右边(左边同理可证),
BD2×PC+CD2×PB
=BD2×(CD+PD)+CD2×(BD-DP)
=BD2×CD+CD2×BD+PD(BD2-CD2)
=BD×CD×(BD+CD)+PD×(BD+CD)×(BD-CD)
=BD×CD×BC+DP×BC×(BD-CD)
=BC×(BD×CD-DP×CD+DP×BD)
=BC×(BP×CD+DP×BD)
=BC×(BP×CD+DP×BP+DP×DP)
=BC×(BP×CP+DP2),
∴AB2×PC+AC2×PB
=BC×AD2+BD2×PC+CD2×PB
=BC×AD2+BC×(BP×CP+DP2)
=BC×(AD2+DP2+BP×CP)
=BC×(AP2+PB×PC),
即AB2×PC+AC2×PB=BC×(AP2+PB×PC).
点评:考查了勾股定理,解决本题的关键是作出辅助线构造直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.
今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.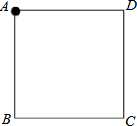 一枚棋子依次沿正方形ABCD的四个顶点A、B、C、D、A、B、C、D…移动,开始时棋子在A点(如图),然后根据骰子所掷点数移动棋子(如掷了1点,则移动1格到B,如掷6点,则移动6格到C等),移动后到达的点为新的出发点,再次进行同样的游戏.
一枚棋子依次沿正方形ABCD的四个顶点A、B、C、D、A、B、C、D…移动,开始时棋子在A点(如图),然后根据骰子所掷点数移动棋子(如掷了1点,则移动1格到B,如掷6点,则移动6格到C等),移动后到达的点为新的出发点,再次进行同样的游戏.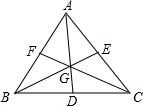 已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证:
已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证: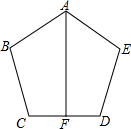 如图,AB=AE,BC=ED,∠B=∠E,求证:∠BCD=∠EDC.
如图,AB=AE,BC=ED,∠B=∠E,求证:∠BCD=∠EDC.