题目内容
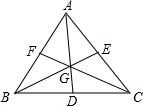 已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证:
已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证:(1)DG=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)以AD,BE,CF为边围成的三角形的面积是△ABC的
| 3 |
| 4 |
考点:三角形的重心
专题:
分析:(1)由于点G是三角形ABC的重心,根据三角形重心的性质可知AG=2DG,又AG+DG=AD,即可证明DG=
AD,同理得到EG=
BE,FG=
CF;
(2)延长AD到M,使DM=AD,连接BM、MC,取BM中点H,连接FH、CH,则四边形ABMC为平行四边形,得AC=BM,又因为E、H分别为AC、BM中点,得BH平行且等于EC,则HC=BE,同理得FH平行且等于AD,得到△FCH三边长即为△ABC三中线长,然后依次求出S△BFH=
S△ABM=
×
S平行四边形ABMC=
S△ABC,S△CAF=
S△ABC,S△CHM=
S△CBM=
S△ABC,最后得到S△FCH=S平行四边形ABMC-S△BHF-S△CHM-S△CAF=2S△ABC-
S△ABC-
S△ABC-
S△ABC.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)延长AD到M,使DM=AD,连接BM、MC,取BM中点H,连接FH、CH,则四边形ABMC为平行四边形,得AC=BM,又因为E、H分别为AC、BM中点,得BH平行且等于EC,则HC=BE,同理得FH平行且等于AD,得到△FCH三边长即为△ABC三中线长,然后依次求出S△BFH=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:(1)∵点G是三角形ABC的三条中线AD,BE,CF的交点,
∴点G是三角形ABC的重心,
∴AG=2DG,
又AG+DG=AD,
∴DG=
AD,
同理EG=
BE,FG=
CF;
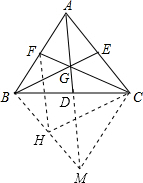 (2)如图,延长AD到M,使DM=AD,连接BM、MC,取BM中点H,连接FH、CH,
(2)如图,延长AD到M,使DM=AD,连接BM、MC,取BM中点H,连接FH、CH,
∵DM=AD,BD=CD,
∴四边形ABMC为平行四边形,
∴AC=BM,
又∵E、H分别为AC、BM中点,
∴BH平行且等于EC,
∴四边形BHCE为平行四边形,
∴HC=BE,
又∵F、H为AB、BM中点,
∴FH平行且等于
AM,
∴FH平行且等于AD,
∴△FCH三边长即为△ABC三中线长,
又∵△BHF∽△BMA,
=
,
∴S△BFH=
S△ABM=
×
S平行四边形ABMC=
S△ABC,
∵S△CAF=
S△ABC,S△CHM=
S△CBM=
S△ABC,
∴S△FCH=S平行四边形ABMC-S△BHF-S△CHM-S△CAF=2S△ABC-
S△ABC-
S△ABC-
S△ABC=
S△ABC.
∴点G是三角形ABC的重心,
∴AG=2DG,
又AG+DG=AD,
∴DG=
| 1 |
| 3 |
同理EG=
| 1 |
| 3 |
| 1 |
| 3 |
 (2)如图,延长AD到M,使DM=AD,连接BM、MC,取BM中点H,连接FH、CH,
(2)如图,延长AD到M,使DM=AD,连接BM、MC,取BM中点H,连接FH、CH,∵DM=AD,BD=CD,
∴四边形ABMC为平行四边形,
∴AC=BM,
又∵E、H分别为AC、BM中点,
∴BH平行且等于EC,
∴四边形BHCE为平行四边形,
∴HC=BE,
又∵F、H为AB、BM中点,
∴FH平行且等于
| 1 |
| 2 |
∴FH平行且等于AD,
∴△FCH三边长即为△ABC三中线长,
又∵△BHF∽△BMA,
| BF |
| AB |
| 1 |
| 2 |
∴S△BFH=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∵S△CAF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△FCH=S平行四边形ABMC-S△BHF-S△CHM-S△CAF=2S△ABC-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题考查了三角形重心的性质,相似三角形的判定与性质,平行四边形的判定与性质,有一定难度.准确作出辅助线,得出△FCH是以AD,BE,CF为边围成的三角形是解第(2)题的关键.

练习册系列答案
相关题目
 如图所示,在△ABC中,P是BC边上的一点,试说明AB2•PC+AC2•PB=BC(AP2+PB•PC).
如图所示,在△ABC中,P是BC边上的一点,试说明AB2•PC+AC2•PB=BC(AP2+PB•PC). 如图,一艘海上巡逻船在A巡航,这时接到B海上指挥中心紧急通知:在指挥中心北偏西60°方向的C有一艘渔船遇险,要求马上前去救援.此时C位于A北偏西30°方向上,A位于B北偏西75°方向上.AB之间的距离为12.求A、C两地之间的距离.(参考数据:
如图,一艘海上巡逻船在A巡航,这时接到B海上指挥中心紧急通知:在指挥中心北偏西60°方向的C有一艘渔船遇险,要求马上前去救援.此时C位于A北偏西30°方向上,A位于B北偏西75°方向上.AB之间的距离为12.求A、C两地之间的距离.(参考数据: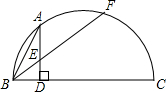 如图所示,BC是⊙O直径,AD⊥BC,垂足为D,
如图所示,BC是⊙O直径,AD⊥BC,垂足为D,