题目内容
 今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.
今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.(1)设购买甲种树苗x棵,甲种树苗每棵m元,根据信息填表(用含x,m代数式表示),并求m的值;
| 树苗类型 | 甲种树苗 | 乙种树苗 |
| 买树苗数量(单位:元) | x | 500-x |
| 买树苗的总费用(单位:元) |
考点:二元一次方程组的应用
专题:
分析:(1)利用甲种树苗每棵m元,乙种树苗比甲种树苗每棵多30元,进而得出乙种树苗价格,再利用成活率得出等式,进而求出x的值,即可得出m的值;
(2)利用这批树苗(包括新购买树苗)的成活率能否恰好为93%,得出等式求出即可.
(2)利用这批树苗(包括新购买树苗)的成活率能否恰好为93%,得出等式求出即可.
解答:解:(1)m,(m+30);
90%x+95%(50-x)=500×92%
-0.05x=-15
解得:x=300,
300m+200(m+30)=25600
整理得:500m=19600
解得:m=39.2;
(2)设新购买甲种树苗x棵,乙种树苗Y棵
解得:
则新购买甲种树苗20棵.
故答案为:20.
90%x+95%(50-x)=500×92%
-0.05x=-15
解得:x=300,
300m+200(m+30)=25600
整理得:500m=19600
解得:m=39.2;
(2)设新购买甲种树苗x棵,乙种树苗Y棵
|
解得:
|
则新购买甲种树苗20棵.
故答案为:20.
点评:此题主要考查了二元一次方程组的应用,根据成活率得出等式是解题关键.

练习册系列答案
相关题目
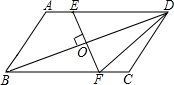 已知:如图,AD∥BC,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.下列结论正确的是( )
已知:如图,AD∥BC,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.下列结论正确的是( )①△BOF≌△DOE;②DE=DF;③BD平分∠ADF;④AE=CF.
| A、①② | B、①③ |
| C、①②③ | D、①②③④ |
 如图所示的图形旋转一定角度后能与自身重合,则旋转的角度可以是( )
如图所示的图形旋转一定角度后能与自身重合,则旋转的角度可以是( )| A、30° | B、45° |
| C、60° | D、90° |
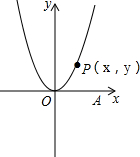 如图,P是抛物线y=x2上第一象限内的点,A点坐标为(6,0).
如图,P是抛物线y=x2上第一象限内的点,A点坐标为(6,0). 如图,点B、F、C、E在一条直线上,FB=CE,AB∥DE,∠A=∠D.猜想并验证线段AC与DF的关系.
如图,点B、F、C、E在一条直线上,FB=CE,AB∥DE,∠A=∠D.猜想并验证线段AC与DF的关系. 如图所示,在△ABC中,P是BC边上的一点,试说明AB2•PC+AC2•PB=BC(AP2+PB•PC).
如图所示,在△ABC中,P是BC边上的一点,试说明AB2•PC+AC2•PB=BC(AP2+PB•PC).