题目内容
14．已知p1=a，pn=1-$\frac{1}{{p}_{n-1}}$（n=1，2，3，…）（1）请分别求出p3，p4；$\frac{-1}{a-1}$，a
（2）则p2018=$\frac{a-1}{a}$．
分析 （1）根据已知条件得到p2=$\frac{a-1}{a}$，p3=$\frac{-1}{a-1}$，p4=a，于是得到结论；
（2）根据（1）中的规律即可得到结果．
解答 解：（1）∵p1=a，
∴p2=1-$\frac{1}{{p}_{1}}$=1-$\frac{1}{a}$=$\frac{a-1}{a}$，
∴p3=1-$\frac{a}{a-1}$=$\frac{-1}{a-1}$，
∴p4=1+（a-1）=a，
故答案为：$\frac{-1}{a-1}$，a；
（2）2018÷3=672…2，
∴p2018=$\frac{a-1}{a}$，
故答案为：$\frac{a-1}{a}$．
点评 本题考查了规律型：数字的变化类，找准规律是解题的关键．
练习册系列答案
相关题目
5．
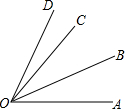如图所示，OB是∠AOC平分线，∠COD=$\frac{1}{3}$∠BOD，∠COD=17°，则∠AOD的度数是（ ）
如图所示，OB是∠AOC平分线，∠COD=$\frac{1}{3}$∠BOD，∠COD=17°，则∠AOD的度数是（ ）| A． | 70° | B． | 83° | C． | 68° | D． | 85° |
2．2017年5月13日，国家互联网应急中心NCNCERT发布《关于中点防范Windows操作系统勒索软件攻击的情况公告》，网络安全引起了人们高度重视，下列网络软件的图标中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
19．下列计算正确的是（ ）
| A． | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B． | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{8-3}$ | C． | $\sqrt{3\frac{2}{3}}$=3$\sqrt{\frac{2}{3}}$ | D． | $\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$ |
6．
某中学八年级的八（一）班、八（二）班分别选5名同学参加“文明创建”知识大赛活动，其预赛成绩如图所示：
（1）根据如图，填写下表．
（2）请从不同的角度对两班的成绩进行分析评价（至少写出三条）；
（3）八（二）班选手飞飞说：“我的成绩是中等水平，”你知道他是几号选手吗？请简述理由．
某中学八年级的八（一）班、八（二）班分别选5名同学参加“文明创建”知识大赛活动，其预赛成绩如图所示：（1）根据如图，填写下表．
| 平均数 | 中位数 | 众数 | 方差 | |
| 八（一）班 | 8.5 | 8.5 | 8.5 | 0.7 |
| 八（二）班 | 8.5 | 8 | 10 | 1.6 |
（3）八（二）班选手飞飞说：“我的成绩是中等水平，”你知道他是几号选手吗？请简述理由．
