题目内容
4.如图,第1个图有2个小三角形,第2个图有6个小三角形,第3个图有12个小三角形…,按此规律,则第n个图有n(n+1)个小三角形.
分析 观察不难发现,每一个图形中小三角形的个数等于图形序号乘以比序号大1的数,根据此规律解答即可.
解答 解:第1个图有2个小三角形,2=1×2,
第2个图有6个小三角形,6=2×3,
第3个图有12个小三角形,12=3×4,
…,
以此类推,第n个图有n(n+1)个小三角形.
故答案为:n(n+1).
点评 本题是对图形变化规律的考查,发现小三角形的个数是两个连续整数的乘积是解题的关键,此类题目对同学们的能力要求较高,在平时的学习中要不断积累.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 如图,菱形ABCD的边长为6,BD=6,E、F分别是边AD、CD上的两个动点,且满足AE+CF=6.
如图,菱形ABCD的边长为6,BD=6,E、F分别是边AD、CD上的两个动点,且满足AE+CF=6.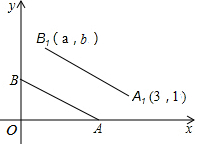 如图所示,A、B的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB.若A1、B1的坐标分别为(3,1),(a,b),则a+b的值为( )
如图所示,A、B的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB.若A1、B1的坐标分别为(3,1),(a,b),则a+b的值为( ) 如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.