题目内容
 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.(1)求OM的长;
(2)求弦CD的长.
考点:垂径定理,勾股定理
专题:
分析:(1)作辅助线;首先根据题意求出ON,根据30°角的直角三角形的性质即可求得OM;
(2)借助勾股定理求出CM的长度,即可解决问题.
(2)借助勾股定理求出CM的长度,即可解决问题.
解答: 解:如图,连接OC,则CF=DF;
解:如图,连接OC,则CF=DF;
∵AB=10,
∴OA=5,
∵ON:AN=2:3,
∴ON=2,
∵∠ANC=30°,
∴∠ONM=30°,
∴OM=
ON=1;
(2)由勾股定理得:
CM2=CO2-OM2
=25-1=24,
∴CM=2
,
∴CD=2CM=4
.
 解:如图,连接OC,则CF=DF;
解:如图,连接OC,则CF=DF;∵AB=10,
∴OA=5,
∵ON:AN=2:3,
∴ON=2,
∵∠ANC=30°,
∴∠ONM=30°,
∴OM=
| 1 |
| 2 |
(2)由勾股定理得:
CM2=CO2-OM2
=25-1=24,
∴CM=2
| 6 |
∴CD=2CM=4
| 6 |
点评:本题考查了垂径定理、勾股定理、含30°角的直角三角形的边角关系及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
对二次函数y=-x2-2x+2的图象描述正确的是( )
| A、与x轴有两个交点,对称轴在y轴的右侧 |
| B、与x轴有两个交点,对称轴在y轴的左侧 |
| C、与x轴没有交点,对称轴在y轴的左侧 |
| D、与x轴没有交点,对称轴在y轴的右侧 |
已知实数(x2-x)2-4(x2-x)-12=0,则代数式x2-x+1的值为( )
| A、-1 | B、7 |
| C、-1或7 | D、以上全不正确 |
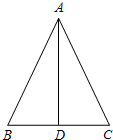 如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,
如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,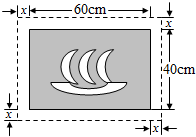 在一幅长60cm、宽40cm的矩形风景画的四周外镶一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是2816cm2,那么金色纸边的宽应为多少cm?
在一幅长60cm、宽40cm的矩形风景画的四周外镶一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是2816cm2,那么金色纸边的宽应为多少cm?
 如图,直线y=kx-2与双曲线y=
如图,直线y=kx-2与双曲线y=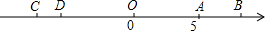 如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.
如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.