题目内容
 如图,直线y=kx-2与双曲线y=
如图,直线y=kx-2与双曲线y=| 3k |
| x |
(1)求AE的长.
(2)求这两个函数的解析式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先根据直线y=kx-2求得OD的长,然后根据△OCD与△OCA的面积比是2:1即可求得AE的长;
(2)把点A的纵坐标分别代入y=kx-2与y=
,即可求得k的值,进而就可求得两个函数的解析式.
(2)把点A的纵坐标分别代入y=kx-2与y=
| 3k |
| x |
解答:解:(1)当x=0时,y=kx-2=-2,即OD=2.
∵
=
=
=
∴AE=1.
(2)∵AE=1,
∴点A的纵坐标为1,
∴y=kx-2=1,y=
=1
解得k=1(舍),k=-1
∴这两个函数的解析式分别为y=-x-2,y=
.
∵
| S△OCD |
| S△OCA |
| ||
|
| OD |
| AE |
| 2 |
| 1 |
∴AE=1.
(2)∵AE=1,
∴点A的纵坐标为1,
∴y=kx-2=1,y=
| 3k |
| x |
解得k=1(舍),k=-1
∴这两个函数的解析式分别为y=-x-2,y=
| -3 |
| x |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.

练习册系列答案
相关题目
如图,每个图案均由边长为1的小正方形按一定的规律堆叠而成,照此规律,第10个图案中共有( )个小正方形.


| A、50 | B、80 |
| C、100 | D、120 |
若△ABC∽△A1B1C1,其面积比为
,△A1B1C1与△ABC的周长比为( )
| 4 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )
| A、1,2,3 |
| B、2,3,4 |
| C、5,12,13 |
| D、4,5,6 |
 如图△ABC中,AD⊥BC于D,AB=13,AD=12,BC=14,求AC的长.
如图△ABC中,AD⊥BC于D,AB=13,AD=12,BC=14,求AC的长. 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M. 如图,已知正比例函数y=2x和反比例函数的图象交于点 A(m,-2).
如图,已知正比例函数y=2x和反比例函数的图象交于点 A(m,-2).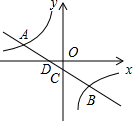 如图,一次函数y=kx+b的图象与反比例函数
如图,一次函数y=kx+b的图象与反比例函数 已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE=
已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE=