题目内容
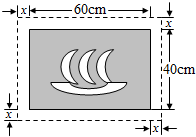 在一幅长60cm、宽40cm的矩形风景画的四周外镶一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是2816cm2,那么金色纸边的宽应为多少cm?
在一幅长60cm、宽40cm的矩形风景画的四周外镶一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是2816cm2,那么金色纸边的宽应为多少cm?考点:一元二次方程的应用
专题:几何图形问题
分析:根据题意可知:矩形挂图的长为(60+2x)cm,宽为(40+2x)cm;则运用面积公式列方程求解即可.
解答:解:挂图长为(60+2x)cm,宽为(40+2x)cm,
所以根据矩形的面积公式可得:(60+2x)(40+2x)=2816.
解得:x=2或x=-52(舍去).
答:金色纸边的宽应为2cm.
所以根据矩形的面积公式可得:(60+2x)(40+2x)=2816.
解得:x=2或x=-52(舍去).
答:金色纸边的宽应为2cm.
点评:此题是一元二次方程的应用,解此类题的关键是看准题型列面积方程,矩形的面积=矩形的长×矩形的宽.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列说法错误的是( )
| A、全等三角形的对应边相等 |
| B、全等三角形的角相等 |
| C、全等三角形的周长相等 |
| D、全等三角形的面积相等 |
若△ABC∽△A1B1C1,其面积比为
,△A1B1C1与△ABC的周长比为( )
| 4 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,直线a,b被直线c所截,a∥b,∠1=110°,∠2=
如图所示,直线a,b被直线c所截,a∥b,∠1=110°,∠2= 如图△ABC中,AD⊥BC于D,AB=13,AD=12,BC=14,求AC的长.
如图△ABC中,AD⊥BC于D,AB=13,AD=12,BC=14,求AC的长. 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.