题目内容
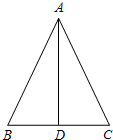 如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,
如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,(1)求AC;
(2)若点P在边AC上移动,则BP的最小值是
考点:勾股定理,垂线段最短
专题:
分析:(1)先根据BC=16,AD是BC的中线求出BD的长,再根据勾股定理的逆定理判断出△ABD的形状,根据勾股定理即可得出AC的长;
(2)根据三角形的面积公式即可得出BP的最小值.
(2)根据三角形的面积公式即可得出BP的最小值.
解答:解:(1)∵在△ABC中,AB=17,BC=16,BC边上的中线AD=15,
∴BD=CD=
BC=8,
∵152+82=172,
∴△ABD是直角三角形,即∠ADB=90°.
∴AC=
=
=17;
(2)∵当BP⊥AC时,BP最短,
∴AC•BP=BC•AD,
∴BP=
=
=
.
故答案为:
.
∴BD=CD=
| 1 |
| 2 |
∵152+82=172,
∴△ABD是直角三角形,即∠ADB=90°.
∴AC=
| AD2+CD2 |
| 152+82 |
(2)∵当BP⊥AC时,BP最短,
∴AC•BP=BC•AD,
∴BP=
| BC•AD |
| AC |
| 16×15 |
| 17 |
| 120 |
| 17 |
故答案为:
| 120 |
| 17 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
△ABC的三边长是a、b、c,且b=5,c=2,则a的取值范围是( )
| A、3<a<7 |
| B、5<a<7 |
| C、7<a<14 |
| D、2<a<5 |
 如图,每个面上都有一个汉字的正方体的一种展开图,那么在原正方体“着”相对的面上的汉字是
如图,每个面上都有一个汉字的正方体的一种展开图,那么在原正方体“着”相对的面上的汉字是 如图所示,直线a,b被直线c所截,a∥b,∠1=110°,∠2=
如图所示,直线a,b被直线c所截,a∥b,∠1=110°,∠2= 如图,在等腰△ABC中,AB=AC,AD是底边BC上的高线,若AB=10,BC=12,求AD的长.
如图,在等腰△ABC中,AB=AC,AD是底边BC上的高线,若AB=10,BC=12,求AD的长. 如图△ABC中,AD⊥BC于D,AB=13,AD=12,BC=14,求AC的长.
如图△ABC中,AD⊥BC于D,AB=13,AD=12,BC=14,求AC的长. 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.