题目内容
 如图,梯形ABCD中,AD∥BC,∠BAD=90°,AD=7cm,BC=4cm,AB=4cm,现有动点P以3cm/s的速度从点A向点D运动,动点Q以2cm/s的速度从点C向点B运动,若P,Q两点同时出发,一个点停止运动时另一个点也停止运动,连接AQ、PQ,设运动时间为x s,请问x为何值时,△APQ为等腰三角形.
如图,梯形ABCD中,AD∥BC,∠BAD=90°,AD=7cm,BC=4cm,AB=4cm,现有动点P以3cm/s的速度从点A向点D运动,动点Q以2cm/s的速度从点C向点B运动,若P,Q两点同时出发,一个点停止运动时另一个点也停止运动,连接AQ、PQ,设运动时间为x s,请问x为何值时,△APQ为等腰三角形.考点:梯形
专题:动点型
分析:利用当AQ=AP时,当AQ=QP时,当QP=AP时,利用勾股定理结合矩形的性质分别求出即可.
解答:
解:①如图1,
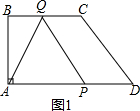
当x秒时,AQ=AP,则QC=2x,AP=3x,
故AQ=3x,则AB2+BQ2=AQ2,即42+(4-2x)2=(3x)2,
解得:x1=
,x2=
(不合题意舍去);
即
秒时AQ=AP,△APQ为等腰三角形;
②如图2,
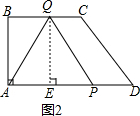
设当t秒时AQ=QP,过点Q作QE⊥AD于点E,
∵AQ=QP,QE⊥AP,
∴AE=EP,
∴BQ=AE,则QC=2t,BQ=AE=4-2t,AP=3t,
故
=4-2t,
解得:t=
,
即
秒时,AQ=QP,△APQ为等腰三角形;
③如图3,
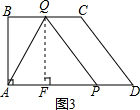
设当y秒时QP=AP,过点Q作QF⊥AD于点F,
则BQ=AF=4-2y,PF=3y-(4-2y)=5y-4,QP=AP=3y,
故PF2+QF2=QP2,
则(5y-4)2+42=(3y)2,
整理得:4y2-5y+8=0,
b2-4ac=25-126=-101<0,故此方程无实数根,
则QP≠AP.
综上所述:
秒或
秒时,△APQ为等腰三角形.

当x秒时,AQ=AP,则QC=2x,AP=3x,
故AQ=3x,则AB2+BQ2=AQ2,即42+(4-2x)2=(3x)2,
解得:x1=
-8+2
| ||
| 5 |
-8-2
| ||
| 5 |
即
-8+2
| ||
| 5 |
②如图2,

设当t秒时AQ=QP,过点Q作QE⊥AD于点E,
∵AQ=QP,QE⊥AP,
∴AE=EP,
∴BQ=AE,则QC=2t,BQ=AE=4-2t,AP=3t,
故
| 3t |
| 2 |
解得:t=
| 8 |
| 7 |
即
| 8 |
| 7 |
③如图3,

设当y秒时QP=AP,过点Q作QF⊥AD于点F,
则BQ=AF=4-2y,PF=3y-(4-2y)=5y-4,QP=AP=3y,
故PF2+QF2=QP2,
则(5y-4)2+42=(3y)2,
整理得:4y2-5y+8=0,
b2-4ac=25-126=-101<0,故此方程无实数根,
则QP≠AP.
综上所述:
-8+2
| ||
| 5 |
| 8 |
| 7 |
点评:此题主要考查了梯形以及勾股定理和一元二次方程的解法,利用分类讨论得出是解题关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
三角形中,到三个顶点距离相等的点是( )
| A、三条高线的交点 |
| B、三条中线的交点 |
| C、三条角平分线的交点 |
| D、三边垂直平分线的交点 |
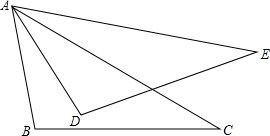 如图,使△ABC≌△ADE的条件是( )
如图,使△ABC≌△ADE的条件是( )| A、∠BAC=∠DAE,∠ABC=∠ADE,∠ACB=∠AED |
| B、∠BAC=∠DAE,AB=AD,BC=DE |
| C、∠BAD=∠CAE,AB=AD,AC=AE |
| D、∠ACB=∠AED,AB=AD,AC=AE |
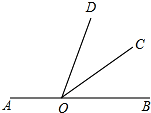 如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=36°,则∠AOD等于( )
如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=36°,则∠AOD等于( )| A、72° | B、100° |
| C、108° | D、144° |
 如图,矩形ABCD中,AB=1,AD=a,以点A为圆心,a为半径画弧,交BC于点E,交AB延长线于点F,当两个阴影部分面积相等时,a的值是
如图,矩形ABCD中,AB=1,AD=a,以点A为圆心,a为半径画弧,交BC于点E,交AB延长线于点F,当两个阴影部分面积相等时,a的值是 如图,点A在反比例函数y=
如图,点A在反比例函数y= 如图所示的各边相等的正五角星中,∠A=α、∠CGH=β、∠HIJ=γ,则α:β:γ=
如图所示的各边相等的正五角星中,∠A=α、∠CGH=β、∠HIJ=γ,则α:β:γ=