题目内容
10．解不等式组：$\left\{\begin{array}{l}\frac{x-3}{2}+3≥8\\ 1-3（x-1）＜8-x\end{array}\right.$（注：必须通过画数轴求解集）分析 根据一元一次不等式的解法分别解出两个不等式，根据不等式的解集的确定方法得到不等式组的解集．
解答 解：$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥8①}\\{1-3（x-1）＜8-x②}\end{array}\right.$，
由①得x≥13，
由②得x＞-2，
所以原不等式组的解是：x≥13．
点评 本题考查的是一元一次不等式组的解法，掌握确定解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到是解题的关键．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1．若a＞b，则下列不等式正确的是（ ）
| A． | a＞-b | B． | a＜-b | C． | 2-a＞a-b | D． | -2a＜-2b |
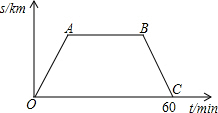星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼，她连续、匀速走了60min后回家，图中的折线段OA-AB-BC是她出发后所在位置离家的距离s（km）与行走时间t（min）之间的函数关系，则下列图形中可以大致描述蕊蕊妈妈行走的路线是（ ）
小丽的家和学校在一条笔直的马路旁，某天小丽沿着这条马路上学，先从家步行到公交站台甲，再乘车到公交站如乙下车，最后步行到学校（在整个过程中小丽步行的速度不变）．图中折线ABCDE表示小丽和学校之间的距离y（米）与她离家时间x（分钟）之间的函数关系．