题目内容
18.若$\sqrt{{x}^{2}}$=-x,则x≤0.分析 根据二次根式的性质即可得出结论.
解答 解:∵$\sqrt{{x}^{2}}$=-x,
∴x≤0.
故答案为:≤0.
点评 本题考查的是二次根式的性质与化简,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
8.(x-2y)(x+2y)的结果是( )
| A. | x2-2y2 | B. | x2-4y2 | C. | x2+4xy+4y2 | D. | x2-4xy+4y2 |
10. 如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )
如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )
 如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )
如图,那么|a-b|+$\sqrt{(a+b)^{2}}$的结果是( )| A. | -2b | B. | 2b | C. | -2a | D. | 2a |
7.在实数-2$\sqrt{5}$、0、-5、3中,最小的实数是( )
| A. | -2$\sqrt{5}$ | B. | 0 | C. | -5 | D. | 3 |
8.某煤矿原计划x天生存120t煤,由于采用新的技术,每天增加生存3t,因此提前2天完成,列出的方程为( )
| A. | $\frac{120}{x-2}$=$\frac{120}{x}$=-3 | B. | $\frac{120}{x}=\frac{120}{x+2}$-3 | C. | $\frac{120}{x+2}=\frac{120}{x}$-3 | D. | $\frac{120}{x}$=$\frac{120}{x-2}$-3 |
 将一组整数按如图所示的规律排列下去,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )
将一组整数按如图所示的规律排列下去,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )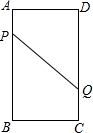 A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.
A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.