题目内容
3.菱形ABCD中,∠B=60°,AB=4,点E在BC上,CE=2$\sqrt{3}$,若点P是菱形上异于点E的另一点,CE=CP,则EP的长为6或2$\sqrt{6}$或2$\sqrt{3}$-$\sqrt{6}$.分析 连接EP交AC与点H,依据菱形的性质可得到∠ECH=∠PCH=60°,然后依据SAS可证明△ECH≌△PCH,则∠EHC=∠PHC=90°,最后依据PE=EH=2sin60°•EC求解即可.
解答 解:如图所示:连接EP交AC与点H.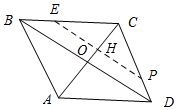
∵菱形ABCD中,∠B=60°,
∴∠BCD=120°,∠ECH=∠PCH=60°.
在△ECH和△PCH中$\left\{\begin{array}{l}{EC=PC}\\{∠ECH=∠PCH}\\{CH=CH}\end{array}\right.$,
∴△ECH≌△PCH.
∴∠EHC=∠PHC=90°,EH=PH.
∴EP=2EH=2sin60°•EC=2×$\frac{\sqrt{3}}{2}$×2$\sqrt{3}$=6.
如图2所示:△ECP为等腰直角三角形,则EP=$\sqrt{2}$EC=2$\sqrt{6}$.
过点P′作P′F⊥BC.
∵P′C=2$\sqrt{3}$,BC=4,∠B=60°,
∴P′C⊥AB.
∴∠BCP′=30°.
∴FC=$\frac{\sqrt{3}}{2}$×2$\sqrt{3}$=3,P′F=$\sqrt{3}$,EF=2$\sqrt{3}$-3.
∴EP′=$\sqrt{(2\sqrt{3}-3)^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$-$\sqrt{6}$.
故答案为:6或2$\sqrt{6}$或2$\sqrt{3}$-$\sqrt{6}$.
点评 本题主要考查的是菱形的性质,熟练掌握菱形的性质是解题的关键.

练习册系列答案
相关题目
18.已知抛物线y=a(x-1)(x-3)-2(a≠0)与x轴交点的横坐标为m,n,且m<n,又点(x0,y0)是抛物线上一点,则下列结论正确的是( )
| A. | 该抛物线可由抛物线y=ax2向右平移2个单位,向下平移2个单位得到 | |
| B. | 若1<m<n<3,则a>0 | |
| C. | 若1<x0<3,则y0<0 | |
| D. | 不论a取何值,m+n=4 |
15. 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )| A. | 5cm | B. | $2\sqrt{5}$cm | C. | 2$\sqrt{3}$cm | D. | $3\sqrt{5}$cm |
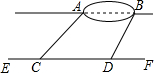 某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.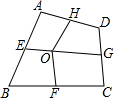 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( )
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( ) 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )