题目内容
9.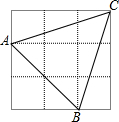 如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题:
如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题:(1)△ABC的周长是多少?
(2)BC边上高是多少?(结果用最简二次根式表示)
分析 (1)利用勾股定理求得△ABC的三边的边长,然后计算其周长;
(2)利用面积法来求BC边上高.
解答 解:(1)如图所示,AB=2$\sqrt{2}$,AC=BC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,则△ABC的周长是:AB+AC+BC=2$\sqrt{2}$+2$\sqrt{10}$;
(2)设BC边上高是h,则
$\frac{1}{2}$BCh=32-$\frac{1}{2}$×2×2-2×$\frac{1}{2}$×1×3=4,
即:$\frac{1}{2}$×$\sqrt{10}$h=4,
解得h=$\frac{4\sqrt{10}}{5}$.
点评 本题考查了二次根式的应用和勾股定理.此题利用了“分割法”来求得三角形ABC的面积.

练习册系列答案
相关题目
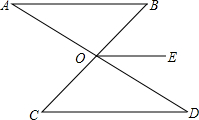 已知:如图,AB∥CD∥OE,∠A=30°,∠C=40°,求:∠AOC的度数.
已知:如图,AB∥CD∥OE,∠A=30°,∠C=40°,求:∠AOC的度数.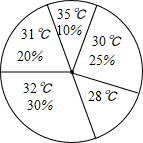 某地连续统计了60天的日最高气温,并绘制了如图所示的扇形统计图,根据统计图可知这60天日最高气温的平均值为31℃.
某地连续统计了60天的日最高气温,并绘制了如图所示的扇形统计图,根据统计图可知这60天日最高气温的平均值为31℃. 如图,将点A向左侧移动3个单位,得到的点所表示的数是-1.
如图,将点A向左侧移动3个单位,得到的点所表示的数是-1.