题目内容
18.($\sqrt{24}+\sqrt{12}$)-(6$\sqrt{\frac{1}{3}}+2\sqrt{6}$)分析 先去括号,把各根式化为最减二次根式,再合并同类项即可.
解答 解:原式=$\sqrt{24}$+$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$-2$\sqrt{6}$
=2$\sqrt{6}$+2$\sqrt{3}$-2$\sqrt{3}$-2$\sqrt{6}$
=0.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
3.方程3x2+5x+1=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
8. 某班50名同学分别站在同一公路上相距1000米的M、N两点处,M处有30人,N处有20人,要让两处的同学集合到一起,并且使所有同学走的路程总和最小,那么集合地点应选在( )
某班50名同学分别站在同一公路上相距1000米的M、N两点处,M处有30人,N处有20人,要让两处的同学集合到一起,并且使所有同学走的路程总和最小,那么集合地点应选在( )
 某班50名同学分别站在同一公路上相距1000米的M、N两点处,M处有30人,N处有20人,要让两处的同学集合到一起,并且使所有同学走的路程总和最小,那么集合地点应选在( )
某班50名同学分别站在同一公路上相距1000米的M、N两点处,M处有30人,N处有20人,要让两处的同学集合到一起,并且使所有同学走的路程总和最小,那么集合地点应选在( )| A. | M点处 | B. | N点处 | ||
| C. | 线段MN的中点处 | D. | 线段MN上,距M点400米处 |
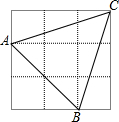 如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题:
如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题: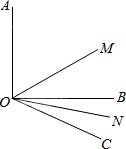 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;