题目内容
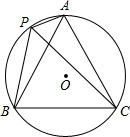 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°(1)请判断△ABC的形状并证明你的结论;
(2)请给出一个能反映PA、PB和PC的数量关系的一个等式,并说明你给出的等式成立;
(3)若PA、PB的长是方程x2-4x+m=0的两个相等的实数根,求⊙O的直径长.
考点:全等三角形的判定与性质,根与系数的关系,垂径定理,圆周角定理
专题:
分析:(1)根据在同圆或等圆中,同弧所对的圆周角相等可得∠ABC=∠APC,∠BAC=∠CPB,然后求出∠BAC=∠ABC=∠ACB,再根据三个角相等的三角形是等边三角形判定;
(2)在PC上截取PD=AP,得到△APD是等边三角形,根据等边三角形的性质可得∠PAD=60°,AP=AD,再求出∠PAB=∠DAC,然后利用“边角边”证明△APB和△ADC全等,根据全等三角形对应边相等可得PB=CD,然后根据PD+CD=PC等量代换即可得解;
(3)利用根与系数的关系求出方程的两个相等实数根,再根据等腰三角形和垂径定理判断出PC是⊙O的直径,然后利用(2)的结论求解即可.
(2)在PC上截取PD=AP,得到△APD是等边三角形,根据等边三角形的性质可得∠PAD=60°,AP=AD,再求出∠PAB=∠DAC,然后利用“边角边”证明△APB和△ADC全等,根据全等三角形对应边相等可得PB=CD,然后根据PD+CD=PC等量代换即可得解;
(3)利用根与系数的关系求出方程的两个相等实数根,再根据等腰三角形和垂径定理判断出PC是⊙O的直径,然后利用(2)的结论求解即可.
解答:解:(1)△ABC是等边三角形.
理由如下:∵∠APC=∠CPB=60°,
∴∠ABC=∠APC=60°,∠BAC=∠CPB=60°,
∴∠BAC=∠ABC=∠ACB,
∴△ABC是等边三角形.
(2)如图,在PC上截取PD=AP,
∵∠APC=60°,
∴△APD是等边三角形,
∴∠PAD=60°,AP=AD,
∵∠PAB+∠BAD=∠DAC+∠BAD=60°,
∴∠PAB=∠DAC,
在△APB和△ADC中,
,
∴△APB≌△ADC(SAS),
∴PB=CD,
∵PD+CD=PC,
∴PA+PB=PC;
(3)∵PA、PB的长是方程x2-4x+m=0的两个相等的实数根,
∴PA=PB=-
=2,
∵∠APC=∠CPB=60°,
∴PC垂直平分AB,
∴PC是⊙O的直径,
∴⊙O的直径长=PA+PB=2+2=4.
理由如下:∵∠APC=∠CPB=60°,
∴∠ABC=∠APC=60°,∠BAC=∠CPB=60°,
∴∠BAC=∠ABC=∠ACB,
∴△ABC是等边三角形.
(2)如图,在PC上截取PD=AP,

∵∠APC=60°,
∴△APD是等边三角形,
∴∠PAD=60°,AP=AD,
∵∠PAB+∠BAD=∠DAC+∠BAD=60°,
∴∠PAB=∠DAC,
在△APB和△ADC中,
|
∴△APB≌△ADC(SAS),
∴PB=CD,
∵PD+CD=PC,
∴PA+PB=PC;
(3)∵PA、PB的长是方程x2-4x+m=0的两个相等的实数根,
∴PA=PB=-
| -4 |
| 2×1 |
∵∠APC=∠CPB=60°,
∴PC垂直平分AB,
∴PC是⊙O的直径,
∴⊙O的直径长=PA+PB=2+2=4.
点评:本题考查了全等三角形的判定与性质,等边三角形的判定与性质,圆周角定理,垂径定理,根与系数的关系,难点在于(3)作辅助线构造成全等三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
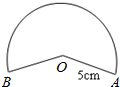 小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,面积是15πcm2,那么这个的圆锥底面半径是( )
小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,面积是15πcm2,那么这个的圆锥底面半径是( )| A、2cm | B、3cm |
| C、4cm | D、5cm |
 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为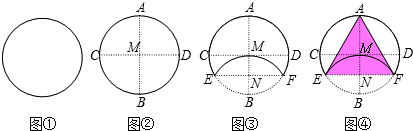
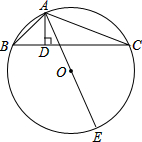 如图,△ABC内接于⊙O,AD⊥BC,AE是⊙O的直径.
如图,△ABC内接于⊙O,AD⊥BC,AE是⊙O的直径. 如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与点D重合,已知AB=3cm,AD=9cm.求EF的长.
如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与点D重合,已知AB=3cm,AD=9cm.求EF的长. 如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.
如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.