题目内容
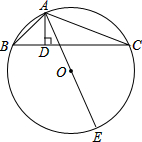 如图,△ABC内接于⊙O,AD⊥BC,AE是⊙O的直径.
如图,△ABC内接于⊙O,AD⊥BC,AE是⊙O的直径.(1)求证:AB•AC=AD•AE;
(2)当AB=
| 2 |
| 2 |
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)连接BE,由AD是⊙O的内接△ABC的高,AE是⊙O的直径,可得∠ABE=∠ADC=90°,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,可得∠E=∠C,即可证得△ABE∽△ADC,然后由相似三角形的对应边成比例,证得AB•AC=AD•AE.
(2)由(1)AB•AC=AD•AE得到AB:AE=AD:AC,结合勾股定理可以求得答案.
(2)由(1)AB•AC=AD•AE得到AB:AE=AD:AC,结合勾股定理可以求得答案.
解答: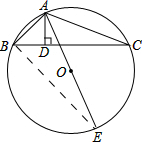 (1)证明:连接BE,
(1)证明:连接BE,
∵AD是⊙O的内接△ABC的高,AE是⊙O的直径,
∴∠ABE=∠ADC=90°,
∵∠E=∠C,
∴△ABE∽△ADC,
∴AB:AD=AE:AC,
∴AB•AC=AD•AE.
(2)解:∵∠EAC=45°,
∴∠B=45°,AB=
,
∴AD=BD=1,
由(1)AB•AC=AD•AE得到:AB:AE=AD:AC=
:4,
∴AC=4,
根据勾股定理得:CD=
=
=
,
所以tan∠ACB=
=
=
.
 (1)证明:连接BE,
(1)证明:连接BE,∵AD是⊙O的内接△ABC的高,AE是⊙O的直径,
∴∠ABE=∠ADC=90°,
∵∠E=∠C,
∴△ABE∽△ADC,
∴AB:AD=AE:AC,
∴AB•AC=AD•AE.
(2)解:∵∠EAC=45°,
∴∠B=45°,AB=
| 2 |
∴AD=BD=1,
由(1)AB•AC=AD•AE得到:AB:AE=AD:AC=
| 2 |
∴AC=4,
根据勾股定理得:CD=
| AC2-AD2 |
| 42-12 |
| 15 |
所以tan∠ACB=
| AD |
| CD |
| 1 | ||
|
| ||
| 15 |
点评:本题考查了相似三角形的判定与性质以及圆周角定理,勾股定理的应用.此题难度适中,注意线段成比例形式的变化.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(a2)3=a5 |
| B、a6÷a3=a2 |
| C、a2•a=a3 |
| D、(a-b)2=a2-b2 |
下列运算中,正确的是( )
| A、x2+x2=x4 |
| B、x6÷x2=x3 |
| C、x2•x4=x6 |
| D、(3x2)2=6x4 |
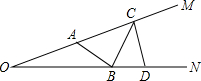 如图,∠MON=20°,A为射线OM上一点,OA=4,D为射线ON上一点,OD=8,C为射线AM上任意一点,B是线段OD上任意一点,那么折线ABCD的长AB+BC+CD的最小值是
如图,∠MON=20°,A为射线OM上一点,OA=4,D为射线ON上一点,OD=8,C为射线AM上任意一点,B是线段OD上任意一点,那么折线ABCD的长AB+BC+CD的最小值是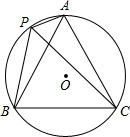 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°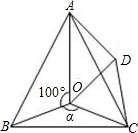 如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.
如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.