题目内容
 如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.
如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.①图中有
②若正方形的边长为1,P为AB的三等分点,求△BHQ的面积.
③求证:DH⊥HQ.
考点:正方形的性质,勾股定理,相似三角形的判定与性质
专题:
分析:①△PHB与△PBC,△PHB与△HBC,△CHB与△PBC,△BHQ与△DHC.
②作HE⊥BC,由P为AB的三等分点,求得BP=
,在Rt△PBC中,由勾股定理得PC=
,由BP•BC=BH•PC,得BH=
=
,在Rt△BHC中,由勾股定理得CH=
,由BH•CH=HE•BC,可得HE=
,解得△BHQ的面积.
③要证QH⊥DH,只要证明∠BHQ=∠CHD.由于△PBC是直角三角形,且BH⊥PC,熟知∠PBH=∠PCB,从而∠HBQ=∠HCD,因而△BHQ与△DHC相似.
②作HE⊥BC,由P为AB的三等分点,求得BP=
| 1 |
| 3 |
| ||
| 3 |
| BP•BC |
| PC |
| ||
| 10 |
3
| ||
| 10 |
| 3 |
| 10 |
③要证QH⊥DH,只要证明∠BHQ=∠CHD.由于△PBC是直角三角形,且BH⊥PC,熟知∠PBH=∠PCB,从而∠HBQ=∠HCD,因而△BHQ与△DHC相似.
解答:①解:图中有4对相似三角形.
故答案为:4.
②解:作HE⊥BC,
∵正方形的边长为1,P为AB的三等分点,
∴BP=BQ=
,
在Rt△PBC中,由勾股定理得PC=
,
∵BP•BC=BH•PC,
∴BH=
=
,
在Rt△BHC中,由勾股定理得CH=
,
∵BH•CH=HE•BC,
∴HE=
=
,
∴△BHQ的面积S=
EH•BQ=
×
×
=
③证明:在Rt△PBC中,
∵BH⊥PC,
∴∠PBC=∠PHB=90°,
∴∠PBH=∠PCB.
显然,Rt△PBC∽Rt△BHC,
∴
=
,
由已知,BP=BQ,BC=DC,
∴
=
∴
=
,
∵∠ABC=∠BCD=90°,∠PBH=∠PCB,
∴∠HBQ=∠HCD.
在△HBQ与△HCD中,
∵
=
,∠HBQ=∠HCD,
∴△HBQ∽△HCD,
∴∠BHQ=∠DHC,
∠BHQ+∠QHC=∠DHC+∠QHC.
又∵∠BHQ+∠QHC=90°,
∴∠QHD=∠QHC+∠DHC=90°,
即DH⊥HQ.

故答案为:4.
②解:作HE⊥BC,
∵正方形的边长为1,P为AB的三等分点,
∴BP=BQ=
| 1 |
| 3 |
在Rt△PBC中,由勾股定理得PC=
| ||
| 3 |
∵BP•BC=BH•PC,
∴BH=
| BP•BC |
| PC |
| ||
| 10 |
在Rt△BHC中,由勾股定理得CH=
3
| ||
| 10 |
∵BH•CH=HE•BC,
∴HE=
| BH•CH |
| BC |
| 3 |
| 10 |
∴△BHQ的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 10 |
| 1 |
| 3 |
| 1 |
| 20 |
③证明:在Rt△PBC中,
∵BH⊥PC,
∴∠PBC=∠PHB=90°,
∴∠PBH=∠PCB.
显然,Rt△PBC∽Rt△BHC,
∴
| BH |
| PB |
| HC |
| BC |
由已知,BP=BQ,BC=DC,
∴
| BH |
| BQ |
| HC |
| CD |
| BH |
| CH |
| BQ |
| CD |
∵∠ABC=∠BCD=90°,∠PBH=∠PCB,
∴∠HBQ=∠HCD.
在△HBQ与△HCD中,
∵
| BH |
| CH |
| BQ |
| CD |
∴△HBQ∽△HCD,
∴∠BHQ=∠DHC,
∠BHQ+∠QHC=∠DHC+∠QHC.
又∵∠BHQ+∠QHC=90°,
∴∠QHD=∠QHC+∠DHC=90°,
即DH⊥HQ.

点评:本题考查了相似三角形的性质和判定以及正方形的性质,关键是相似三角形的判定.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
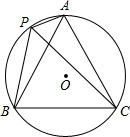 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°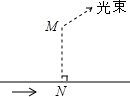 一辆小车沿着水平地面上的长直轨道匀速的向右运动,有一台散发出细光束的激光器装在小转台M上,转台到轨道的距离MN=10米.转台匀速的转动,使激光器在水平面内扫描.扫描一周的时间为60秒,光束转动的方向为逆时针方向.已知当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过2.5秒,光束又射到小车上,求小车的速度?(
一辆小车沿着水平地面上的长直轨道匀速的向右运动,有一台散发出细光束的激光器装在小转台M上,转台到轨道的距离MN=10米.转台匀速的转动,使激光器在水平面内扫描.扫描一周的时间为60秒,光束转动的方向为逆时针方向.已知当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过2.5秒,光束又射到小车上,求小车的速度?(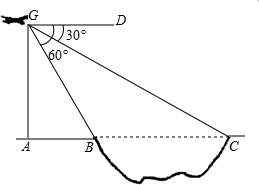 如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?
如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?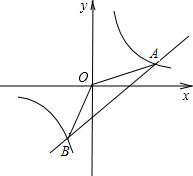 如图,已知A(4,a),B(-2,-4)是一次函数y1=kx+b的图象和反比例函数y2=
如图,已知A(4,a),B(-2,-4)是一次函数y1=kx+b的图象和反比例函数y2=