题目内容
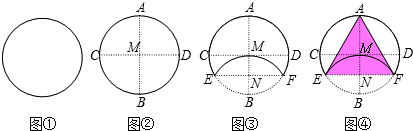
将一张半径为4的圆形纸片(如图①)连续对折两次后展开得折痕AB、CD,且AB⊥CD,垂足为M(如图②),之后将纸片如图③翻折,使点B与点M重合,折痕EF与AB相交于点N,连接AE、AF(如图④),则△AEF的面积是 .

考点:翻折变换(折叠问题)
专题:
分析:连接ME,根据直角三角形30°角所对的直角边等于斜边的一半求出∠MEN=30°,然后求出∠EMN=60°,根据等边对等角求出∠AEM=∠EAM,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠AEM=30°,从而得到∠AEF=60°,同理求出∠AFE=60°,再根据三角形的内角和等于180°求出∠EAF=60°,从而判定△AEF是等边三角形,求出MN、EN,然后求出AN、EF,再根据三角形的面积公式求即可.
解答:解:连接ME,
∵纸片沿EF折叠,B、M两点重合,
∴BN=MN,则ME=MB=2MN,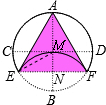
∴∠MEN=30°,
∴∠EMN=90°-30°=60°,
又∵AM=ME(都是半径),
∴∠AEM=∠EAM,
∴∠AEM=
∠EMN=
×60°=30°,
∴∠AEF=∠AEM+∠MEN=30°+30°=60°,
同理可求∠AFE=60°,
∴∠EAF=60°,
∴△AEF是等边三角形,
则MN=
BN=
×4=2,EN=
=2
,
∴EF=2EN=4
,AN=AM+MN=6,
∴△AEF的面积为:
×EF×AN=
×4
×6=12
.
故答案为:12
.
∵纸片沿EF折叠,B、M两点重合,
∴BN=MN,则ME=MB=2MN,

∴∠MEN=30°,
∴∠EMN=90°-30°=60°,
又∵AM=ME(都是半径),
∴∠AEM=∠EAM,
∴∠AEM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEF=∠AEM+∠MEN=30°+30°=60°,
同理可求∠AFE=60°,
∴∠EAF=60°,
∴△AEF是等边三角形,
则MN=
| 1 |
| 2 |
| 1 |
| 2 |
| EM2-MN2 |
| 3 |
∴EF=2EN=4
| 3 |
∴△AEF的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:12
| 3 |
点评:本题圆的综合题型,主要考查了翻折变换的性质,等边三角形的判定与性质,综合题,但难度不大,仔细分析便不难求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算正确的是( )
| A、(a2)3=a5 |
| B、a6÷a3=a2 |
| C、a2•a=a3 |
| D、(a-b)2=a2-b2 |
 如图,在△ABC中,AB=5,AC=4,△ABC绕着点A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之比为
如图,在△ABC中,AB=5,AC=4,△ABC绕着点A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之比为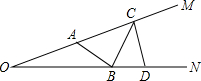 如图,∠MON=20°,A为射线OM上一点,OA=4,D为射线ON上一点,OD=8,C为射线AM上任意一点,B是线段OD上任意一点,那么折线ABCD的长AB+BC+CD的最小值是
如图,∠MON=20°,A为射线OM上一点,OA=4,D为射线ON上一点,OD=8,C为射线AM上任意一点,B是线段OD上任意一点,那么折线ABCD的长AB+BC+CD的最小值是 如图,△ABC,∠A=70°,点D在BC的延长线上,若∠ACD=130°,则∠B=
如图,△ABC,∠A=70°,点D在BC的延长线上,若∠ACD=130°,则∠B=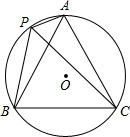 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°