题目内容
 如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与点D重合,已知AB=3cm,AD=9cm.求EF的长.
如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与点D重合,已知AB=3cm,AD=9cm.求EF的长.考点:翻折变换(折叠问题)
专题:
分析:首先由折叠的性质知BE=ED,∠BEG=∠DEG,可得△BDE是等腰三角形,再根据等腰三角形的性质可得BG=GD,BD⊥EF,再在Rt△ABD中,利用勾股定理算出BD的长,再在Rt△ABE中利用勾股定理计算出AE的长,进而得到ED的长,再次利用勾股定理计算出EG的长,然后证明△BGF≌△DGE,继而得到GF=EG,从而得到EF的长.
解答:解:连接BD,交EF于点G.
由折叠的性质知,BE=ED,∠BEG=∠DEG,
∴BG=GD,BD⊥EF.
在Rt△ABD中,BD=
=
=3
,
 ∵BG=DG,
∵BG=DG,
∴DG=
DB=
.
设AE=x,则DE=BE=9-x,
在Rt△ABE中:AE2+AB2=BE2,
则x2+32=(9-x)2,
解得:x=4,
则ED=9-4=5,
在Rt△EDG中:EG2+DG2=ED2,
EG=
=
.
∵BD⊥EF,
∴∠BGF=∠EGD=90°.
∵AD∥CB,
∴∠EDG=∠GBF.
在△BGF与△DGE中,
,
∴△BGF≌△DGE(ASA),
∴GF=EG=
,
∴EF=2EG=
.
由折叠的性质知,BE=ED,∠BEG=∠DEG,
∴BG=GD,BD⊥EF.
在Rt△ABD中,BD=
| AB2+AD2 |
| 32+92 |
| 10 |
 ∵BG=DG,
∵BG=DG,∴DG=
| 1 |
| 2 |
3
| ||
| 2 |
设AE=x,则DE=BE=9-x,
在Rt△ABE中:AE2+AB2=BE2,
则x2+32=(9-x)2,
解得:x=4,
则ED=9-4=5,
在Rt△EDG中:EG2+DG2=ED2,
EG=
52-(
|
| ||
| 2 |
∵BD⊥EF,
∴∠BGF=∠EGD=90°.
∵AD∥CB,
∴∠EDG=∠GBF.
在△BGF与△DGE中,
|
∴△BGF≌△DGE(ASA),
∴GF=EG=
| ||
| 2 |
∴EF=2EG=
| 10 |
点评:此题主要考查了折叠的性质,以及勾股定理的应用,关键是熟练掌握勾股定理:直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC,∠A=70°,点D在BC的延长线上,若∠ACD=130°,则∠B=
如图,△ABC,∠A=70°,点D在BC的延长线上,若∠ACD=130°,则∠B=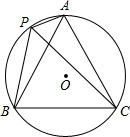 如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°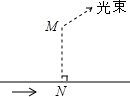 一辆小车沿着水平地面上的长直轨道匀速的向右运动,有一台散发出细光束的激光器装在小转台M上,转台到轨道的距离MN=10米.转台匀速的转动,使激光器在水平面内扫描.扫描一周的时间为60秒,光束转动的方向为逆时针方向.已知当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过2.5秒,光束又射到小车上,求小车的速度?(
一辆小车沿着水平地面上的长直轨道匀速的向右运动,有一台散发出细光束的激光器装在小转台M上,转台到轨道的距离MN=10米.转台匀速的转动,使激光器在水平面内扫描.扫描一周的时间为60秒,光束转动的方向为逆时针方向.已知当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过2.5秒,光束又射到小车上,求小车的速度?(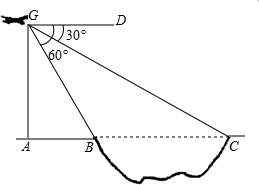 如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?
如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?