题目内容
13.某小区为了绿化环境,计划分两次购进A、B两种花草.第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种草花12棵和5棵,第二次花费265元(两次购进的A、B两种花草价格均分别相同).(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种草花共31棵,且B种花草的数量多于A种花草的数量的7倍,请你给出一种费用最省的方案,并求出该方案所需费用.(两种花草都必须购买)
分析 (1)设A种花草每棵的价格为x元,B种花草每棵的价格为y元,根据“分别购进A、B两种花草30棵和15棵,共花费675元;分别购进A、B两种草花12棵和5棵,共花费265元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买A种花草m棵(m>0),总费用为w元,则购买B种花草(31-m)棵,根据总费用=单价×购买数量,即可得出w关于m的函数关系式,再根据B种花草的数量多于A种花草的数量的7倍,即可求出m的取值范围,根据一次函数的性质即可解决最值问题.
解答 解:(1)设A种花草每棵的价格为x元,B种花草每棵的价格为y元,
根据题意得:$\left\{\begin{array}{l}{30x+15y=675}\\{12x+5y=265}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=5}\end{array}\right.$.
答:A种花草每棵的价格为20元,B种花草每棵的价格为5元.
(2)设购买A种花草m棵(m>0),总费用为w元,则购买B种花草(31-m)棵,
根据题意得:w=20m+5(31-m)=15m+155.
∵31-m>7m,
∴m<3$\frac{7}{8}$,
∵m为正整数,
∴1≤m≤3.
∵w=15m+155中k=15>0,
∴当m=1时,w取最小值,最小值为170.
答:当购买A种花草1棵、B种花草30棵时,所需费用最低,最低费用为170元.
点评 本题考查了二元一次方程组的应用、一次函数的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,列出关于x、y的二元一次方程组;(2)根据总费用=单价×购买数量,找出w关于m的函数关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.一辆小汽车在告诉公路上从静止到起动10秒内的速度经测量如下表:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用时间t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t每增加1秒,v的变化情况相同吗?在哪个时间段内,v增加的最快?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.
| 时间(秒) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 速度(米/秒) | 0 | 0.3 | 1.3 | 2.8 | 1.9 | 7.6 | 11.0 | 14.1 | 18.4 | 24.2 | 28.9 |
(2)如果用时间t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t每增加1秒,v的变化情况相同吗?在哪个时间段内,v增加的最快?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.
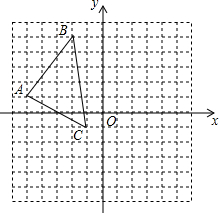 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,每个小正方形边长为1个单位长度.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上,每个小正方形边长为1个单位长度.
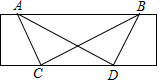 已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.
已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.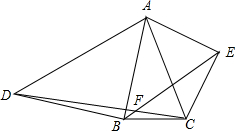 如图,在△ABC中,AB=AC,且∠BAC=30°,以AB为腰作等腰直角三角形ABD,以AC为斜边作等腰直角三角形ACE,连接CD,BE交于点F,求∠DFB的度数.
如图,在△ABC中,AB=AC,且∠BAC=30°,以AB为腰作等腰直角三角形ABD,以AC为斜边作等腰直角三角形ACE,连接CD,BE交于点F,求∠DFB的度数. 等边三角形ABC的面积是30cm2,等边三角形CDE的面积是20cm2,AF=FB,EG=GC,求三角形DFG的面积.
等边三角形ABC的面积是30cm2,等边三角形CDE的面积是20cm2,AF=FB,EG=GC,求三角形DFG的面积.