题目内容
2.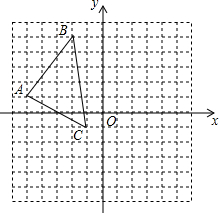 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,每个小正方形边长为1个单位长度.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上,每个小正方形边长为1个单位长度.(1)写出点A、B、C的坐标;
(2)将△ABC向右平移6个单位,再向下平移3个单位得到△A1B1C1,画出图形,并写出各顶点坐标;
(3)求△ABC的面积.
分析 (1)根据A、B、C在坐标系中的位置写出各点坐标即可;
(2)根据平移的规律得到A1,B1,C1点,再顺次连接即可;
(3)根据图形的面积的和差求出△ABC的面积即可.
解答  解:(1)A(-5,1)、B(-2,5)、C(-1,-1);
解:(1)A(-5,1)、B(-2,5)、C(-1,-1);
(2)如图所示,A1(1,-2)、B1(4,2)、C1(5,-4);
(3)S△ABC=6×5-$\frac{1}{2}$×6×1-$\frac{1}{2}×$4×2-$\frac{1}{2}×$3×4=17.
点评 本题考查了利用旋转变换作图,利用平移变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列事件中,发生概率最小的事件的是( )
| A. | 掷一枚普通正六面体骰子所得点数不超过6 | |
| B. | 买一张体育彩票中一等奖 | |
| C. | 从实数-$\frac{2}{7},\sqrt{3},\root{3}{-8},\frac{1}{3}$π,0.1010010001中随机抽取一个数恰好是有理数 | |
| D. | 口袋中装有10 个红球,从中摸出一个是白球 |
17.三元一次方程组$\left\{\begin{array}{l}{x+y=1}\\{y+z=5}\\{z+x=6}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\\{z=0}\end{array}\right.$ |
7.函数y=$\frac{x-2}{x+1}$+x中x的取值范围为( )
| A. | x≠1 | B. | x≠-1 | C. | x≠-2 | D. | x≠2 |
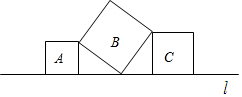 如图,直线l上有三个正方形A,B,C,若正方形A,C的面积分别为6,8,则正方形B的面积为14.
如图,直线l上有三个正方形A,B,C,若正方形A,C的面积分别为6,8,则正方形B的面积为14.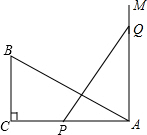 如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由.
如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由. 如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.