题目内容
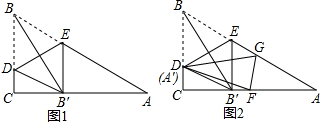
2．
等边三角形ABC的面积是30cm2，等边三角形CDE的面积是20cm2，AF=FB，EG=GC，求三角形DFG的面积．
分析 如图连接CF．只要证明CF∥DG，可得S△DGF=S△DGC=$\frac{1}{2}$S△CDE即可解决问题．
解答 解：如图连接CF．
∵△ABC，△CDE都是等边三角形，AF=BF，EG=CG，
∴∠BCF=$\frac{1}{2}$∠ACB=30°，∠CDG=$\frac{1}{2}$∠CDE=30°，
∴∠BCF=∠CDG，
∴CF∥DG，
∴S△DGF=S△DGC=$\frac{1}{2}$S△CDE=10cm2
点评 本题考查等边三角形的性质．平行线的性质、三角形的面积等知识，解题的关键是学会添加常用辅助线，发现CF∥DG是解题的关键．
练习册系列答案
相关题目
如图，已知：∠1=∠2，AC=AE，BC=DE，且点D在BC上，求证：AB=AD．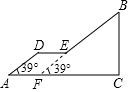
如图，人行天桥的引桥由楼梯和一段水平平台构成，楼梯AD与地面成39°，DE∥AC，楼梯EB与水平地面成39°角，已知BC=6m，AC=11m．
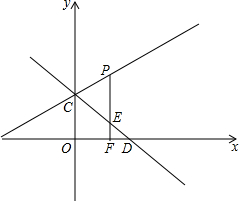如图，直线y=-$\frac{3}{4}$x+3与y轴交于点C，与x轴交于点D，点P是直线y=$\frac{1}{2}$x+3上的一个动点（点P在第一象限），过P作PF⊥x轴于点F，交直线CD于点E，设点P的横坐标为m．
小刘从家里骑自行车出发，去镇上超市途中碰到妹妹甜甜走路从镇上回家，小刘在超市买完东西回家，在回去的路上又碰到了甜甜，便载甜甜一起回家，结果小刘比正常速度回家的时间晚了3分钟，二人离镇的距离S（千米）和小刘从家出发后的时间t（分钟）之间的关系如图所示，（假设二人之间交流时间忽略不计）