题目内容
如图所示，南北方向QP为我国的领海线，以西为公海，晚上10点28分，我边防反偷渡巡逻艇122号在A处发现其正西方向有一只可疑船只C之间的距离为10海里，A、B两艇之间的距离为6海里，B艇与可疑船只C之间的距离为8海里，若该可疑船只的速度为12.8海里/时，问该可疑船只最早在何时进入我国领海？考点：勾股定理的应用
专题：
分析：根据勾股定理的逆定理可得出△ABC是直角三角形，从而判定△CBD∽△CAB，然后利用相似三角形的性质可求出CD的长度，也可求出进入我领海的时间．
解答：解：∵AC=10，AB=6，BC=8，
∴AC2=AB2+BC2，即△ABC是直角三角形，
从而可判断△CBD∽△CAB，
故可得
=
，
解得：CD=
=6.4，
又∵该船只的速度为12.8海里/小时，
∴需要
=0.5小时=30分进入我领海．
即最早晚上10时58分进入我领海．
∴AC2=AB2+BC2，即△ABC是直角三角形，
从而可判断△CBD∽△CAB，
故可得
| BC |
| AC |
| CD |
| CB |
解得：CD=
| 32 |
| 5 |
又∵该船只的速度为12.8海里/小时，
∴需要
| 6.4 |
| 12.8 |
即最早晚上10时58分进入我领海．
点评：此题考查了勾股定理及勾股定理逆定理的知识，解答本题的关键是判断出△ABC是直角三角形，利用相似三角形的性质进行解题．
练习册系列答案
名校课堂系列答案
相关题目
如图，在四边形ABCD中，AB⊥BC，AD⊥DC，连接BD，AC，且DE⊥AC于E，交AB于F，求证：△AFD∽△ADB．
如图所示，九年级某兴趣小组要测量校园内的教学楼AB的高度，在地面上C点用测角仪测得楼顶A点的仰角∠AFE=60°，再沿着直线BC后退8m到达点D，在D点又测得楼顶A的仰角∠AGE=45°，已知测角仪的高度CF为1.6m．求教学楼AB的高度．（结果保留小数点后一位，
如图，已知⊙O的直径AB垂直弦CD于点E，连接CO并延长交AD于点F，若CF⊥AD，AB=2，求DE的长．
如图，AB是圆O的弦，P是AB上一点，AB=10，OP=5，圆O的半径为7，求AP．甲乙两地相距150千米，一辆小汽车和一辆客车同时从两地相向开出，经过50分钟相遇，此时小汽车比客车多行驶30千米．设小汽车和客车的平均速度分别为x千米/小时和y千米/小时．则下列方程组正确的是（ ）
A、
| |||||||||||||
B、
| |||||||||||||
C、
| |||||||||||||
D、
|
-0.8的相反数是（ ）
| A、0.8 | ||
| B、±0.8 | ||
| C、-0.8 | ||
D、
|
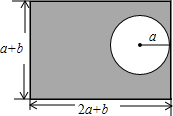某个居民小区的长方形花园的长、宽分别为2a+b和a+b，中间有一个半径为a的圆形游乐场（如图），请你用代数式表示图中阴影部分的面积，再求当a=5米，b=10米时阴影部分面积（π取3.14）．
如图，二次函数y=x2+m的图形与直线y=2x相交于 A、B两点，且C为顶点．若OA：OB=1：2，求m的值．