题目内容
7. 请从以下两个小题中任意选一题作答
请从以下两个小题中任意选一题作答A.如图,正方形CDEF内接于Rt△ABC,点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时正方形CDEF的面积是6.
B.比较大小$\frac{\sqrt{5}-1}{2}$>$\frac{1}{2}$.(填“>”“<”或“=”)
分析 A、首先设正方形CDEF的边长为x,易得△ADE∽△ACB,然后由相似三角形的对应边成比例,求得答案;
B、首先求得$\frac{\sqrt{5}-1}{2}$的近似值,继而比较大小,即可求得答案.
解答 解:A、设正方形CDEF的边长为x,则DE=CF=CD=x,BC=CF+BF=3+x,AC=AD+CD=2+x,
∴DE∥BC,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}=\frac{AD}{AC}$,
∴$\frac{x}{x+3}=\frac{2}{x+2}$,
解得:x=±$\sqrt{6}$,
∴DE=$\sqrt{6}$,
∴正方形CDEF的面积是:6;
B、∵$\frac{\sqrt{5}-1}{2}$≈$\frac{2.236-1}{2}$=0.618,$\frac{1}{2}$=0.5,
∴$\frac{\sqrt{5}-1}{2}$>$\frac{1}{2}$.
故答案为:A、6,B、>.
点评 此题考查了正方形的性质、相似三角形的判定与性质以及实数的比较大小.注意证得△ADE∽△ACB,利用方程思想求解是关键.

练习册系列答案
相关题目
15.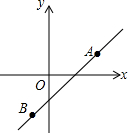 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为( )
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为( )
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为( )
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为( )| A. | -2<x<2 | B. | -1<x<1 | C. | -2<x<1 | D. | -1<x<2 |
2.若x1、x2是方程x2-2x-1=0的两个根,则x1+x1x2+x2的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
19.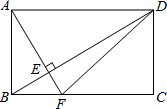 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
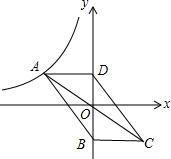 如图,点A在函数y=-$\frac{1}{x}$(x<0)的图象上,将线段AO绕点O按顺时针方向旋转180°后,得到线段CO,若点B、D在y轴上,且AD∥BC∥x轴,则四边形ABCD的面积等于2.
如图,点A在函数y=-$\frac{1}{x}$(x<0)的图象上,将线段AO绕点O按顺时针方向旋转180°后,得到线段CO,若点B、D在y轴上,且AD∥BC∥x轴,则四边形ABCD的面积等于2.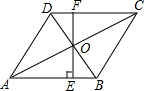 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( ) 如图,已知平面直角坐标系中存在点M(2,0),点A(a,0).在x轴负半轴上有点C,且满足AM=OC,现以AC为对角线作正方形ABCD,设AM的中点为P,当以点O为圆心,OP为半径的圆与正方形ABCD的边相切时,a的值是2$\sqrt{2}$+2或6+4$\sqrt{2}$或6-4$\sqrt{2}$.
如图,已知平面直角坐标系中存在点M(2,0),点A(a,0).在x轴负半轴上有点C,且满足AM=OC,现以AC为对角线作正方形ABCD,设AM的中点为P,当以点O为圆心,OP为半径的圆与正方形ABCD的边相切时,a的值是2$\sqrt{2}$+2或6+4$\sqrt{2}$或6-4$\sqrt{2}$.