题目内容
19．
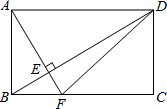如图，在矩形ABCD中，AF⊥BD于E，AF交BC于点F，连接DF，则图中面积相等但不全等的三角形共有（ ）| A． | 2对 | B． | 3对 | C． | 4对 | D． | 5对 |
分析 根据要找出三角形面积相等但不全等的三角形，利用三角形面积公式等底等高面积相等，即可得出答案．
解答 解：∵S△ABD与S△ADF，底边为AD，高为AB，
∴S△ABD=S△ADF
∴S△ABD-S△ADE=S△ABE，
∴S△ABE=S△DEF，
∵S△ABF与S△BDF，底边为BF，高为AB，
∴S△ABF=S△BDF，
S△ADF与S△BCD，等底，等高，
∴S△ADF=S△BDC，
∴图中能确定面积相等但不全等的三角形共有4对，
故选：C．
点评 此题主要考查了矩形的性质以及三角形面积公式应用，根据已知得出三角形的高与底边是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
9．如图1，在矩形ABCD中，AB＜BC，点E为对角线AC上的一个动点，连接BE，DE，过E作EF⊥BC于F．设AE=x，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（ ）
| A． | 线段BE | B． | 线段EF | C． | 线段CE | D． | 线段DE |
请从以下两个小题中任意选一题作答
14．
在西安市开展的“双城联创”活动中，某校倡议七年级学生利用双休日在各自社区参加义务劳动，为了解同学们劳动情况，学校随机抽查了部分学生的劳动时间，并用得到的数据绘制成不完整的统计图表，如图所示：
（1）统计表中的x=40，y=0.18；补全条形统计图．
（2）求所有被调查同学的平均劳动时间．
在西安市开展的“双城联创”活动中，某校倡议七年级学生利用双休日在各自社区参加义务劳动，为了解同学们劳动情况，学校随机抽查了部分学生的劳动时间，并用得到的数据绘制成不完整的统计图表，如图所示：| 劳动时间（时） | 频数（人数） | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
（2）求所有被调查同学的平均劳动时间．
4．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
四边形ABCD的对角线AC、BD相交于点O，AD∥BC，AC=BD．试添加一个条件AB∥CD（答案不唯一），使四边形ABCD为矩形．
8．下列命题是真命题的是（ ）
| A． | 方差越大，说明数据就越稳定 | |
| B． | “预计本题的正确率是95%”表示100位考生中一定有95人做对 | |
| C． | 两边及其一边的对角对应相等的两个三角形一定全等 | |
| D． | 圆内接四边形对角互补 |