题目内容
 如图,等腰△OAB,OA=OB,以O为圆心画圆,与AB、OA、OB分别交于点C、D、E、F,求证:
如图,等腰△OAB,OA=OB,以O为圆心画圆,与AB、OA、OB分别交于点C、D、E、F,求证: |
| EC |
 |
| FD |
考点:全等三角形的判定与性质,垂径定理,圆心角、弧、弦的关系
专题:证明题
分析:连接OC、OD,过O作OM⊥CD于M,根据等腰三角形的性质求出∠AOM=∠BOM,∠COM=∠DOM,求出∠AOC=∠BOD,根据圆周角定理求出即可.
解答:证明: 连接OC、OD,过O作OM⊥CD于M,
连接OC、OD,过O作OM⊥CD于M,
∵OA=OB,OD=OC,
∴∠AOM=∠BOM,∠COM=∠DOM,
∴∠AOM-∠COM=∠BOM-∠DOM,
∴∠AOC=∠BOD,
∴
=
.
 连接OC、OD,过O作OM⊥CD于M,
连接OC、OD,过O作OM⊥CD于M,∵OA=OB,OD=OC,
∴∠AOM=∠BOM,∠COM=∠DOM,
∴∠AOM-∠COM=∠BOM-∠DOM,
∴∠AOC=∠BOD,
∴
 |
| EC |
 |
| FD |
点评:本题考查了等腰三角形的性质,圆周角定理的应用,解此题的关键是求出∠EOC=∠FOD,题目比较好,难度适中.

练习册系列答案
相关题目
已知圆的半径是R,则圆内接正十边形的边长是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知线段l,b和∠α,求作△ABC,使AC=b,∠A=∠α,AB+BC=l.
已知线段l,b和∠α,求作△ABC,使AC=b,∠A=∠α,AB+BC=l.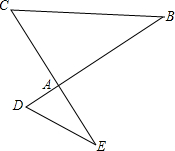 如图,BD、CE相交于点A.
如图,BD、CE相交于点A. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.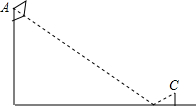 为测量学校操场上旗杆的高度,某数学活动小组设计如下测量方法:将镜子放在离旗杆(AB)27m的点E处,然后沿直线BE后退,使在点D处恰好看到旗杆顶端A在镜子中的像与镜子上的标记重合(如图),若DE=2.4m,观测者的眼睛离地面的高度CD为1.6m,求旗杆的高度.
为测量学校操场上旗杆的高度,某数学活动小组设计如下测量方法:将镜子放在离旗杆(AB)27m的点E处,然后沿直线BE后退,使在点D处恰好看到旗杆顶端A在镜子中的像与镜子上的标记重合(如图),若DE=2.4m,观测者的眼睛离地面的高度CD为1.6m,求旗杆的高度.
 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4cm,将腰CD以D为中心逆时针旋转90°至DE,连结AE、CE,若△ADE的面积是6cm2,则BC=
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4cm,将腰CD以D为中心逆时针旋转90°至DE,连结AE、CE,若△ADE的面积是6cm2,则BC=