题目内容
19. 如图,一块四边形的土地,其中∠DAB=90°,AB=4m,AD=3m,BC=12m,CD=13m,求这块土地的面积?
如图,一块四边形的土地,其中∠DAB=90°,AB=4m,AD=3m,BC=12m,CD=13m,求这块土地的面积?
分析 连接BD,可以求出BD的长,再根据数据的特点得出△BDC也是直角三角形,这样四边形的面积就被分解成了两个直角三角形的面积之和.
解答 解:连接BD
∵AB=4m,AD=3m,∠BAD=90°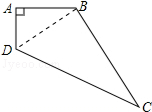
∴BD=$\sqrt{{3}^{2}+{4}^{2}}$=5(m)
∵BC=12m,CD=13m,
∴BD2+CD2=52+122=169,BC2=132,
∴∠DBC=90°,
∴S四边形ABCD=S△ABD+S△BDC=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12=36(m2).
点评 本题考查了勾股定理和勾股定理的逆定理.通过作辅助线,把四边形的面积分解成两个直角三角形的面积来求是解本题的关键所在.

练习册系列答案
相关题目
14. 有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
 有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )| A. | 2a+b | B. | 2a | C. | b | D. | -2a-b |
 请你先在BC上找一点P,使点P到AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.
请你先在BC上找一点P,使点P到AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC. 要求:在下列空白处尺规作图,保留作图痕迹,不写作法,要作答.
要求:在下列空白处尺规作图,保留作图痕迹,不写作法,要作答.