题目内容
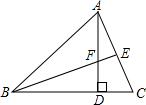 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD=BD.
如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD=BD.求证:AF+DC=BD.
考点:全等三角形的判定与性质
专题:证明题
分析:由在△ABC中,AD⊥BC于点D,BE⊥AC于点E,可得∠BDF=∠ADC=90°与∠DBF=∠DAC,即可证得△BDF≌△ADC(ASA),继而证得:AF+DC=BD.
解答:
证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
,
∴△BDF≌△ADC(ASA),
∴BD=AD,DF=CD,
∴AF+CD=AF+DF=AD=BD.
即AF+DC=BD.
∴∠BDF=∠ADC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
|
∴△BDF≌△ADC(ASA),
∴BD=AD,DF=CD,
∴AF+CD=AF+DF=AD=BD.
即AF+DC=BD.
点评:此题考查了全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 芳芳的妈妈到白佛某市场去买菜,发现把2.5千克的芹菜放到如图所示的度盘秤上时,指针盘上的指针顺时针旋转了90°,由于芹菜和油麦菜的价钱一样,芳芳的妈妈挑选了一些油麦菜放到仍盛有芹菜的度盘秤上,此时的指针又顺时针旋转了108°,则芳芳的妈妈购买的芹菜和油麦菜的总质量为( )
芳芳的妈妈到白佛某市场去买菜,发现把2.5千克的芹菜放到如图所示的度盘秤上时,指针盘上的指针顺时针旋转了90°,由于芹菜和油麦菜的价钱一样,芳芳的妈妈挑选了一些油麦菜放到仍盛有芹菜的度盘秤上,此时的指针又顺时针旋转了108°,则芳芳的妈妈购买的芹菜和油麦菜的总质量为( )| A、3千克 | B、4.5千克 |
| C、5.5千克 | D、6.5千克 |
下列命题中,真命题是( )
| A、相等的角是对顶角 |
| B、两边及一角分别相等的两个三角形全等 |
| C、直角三角形的任意两角互余 |
| D、两角及其夹边分别相等的两个三角形全等 |
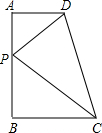 如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=2,AB=6,BC=6,点P是AB上一个动点,则PC+PD的最小值为
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=2,AB=6,BC=6,点P是AB上一个动点,则PC+PD的最小值为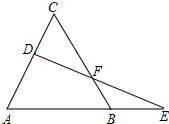 如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.
如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F. 在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,证明:BE2+CF2=EF2.
在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,证明:BE2+CF2=EF2. 二次函数y=ax2+bx+c(a≠0)的图象如图,则函数值y>0时,x的取值范围是
二次函数y=ax2+bx+c(a≠0)的图象如图,则函数值y>0时,x的取值范围是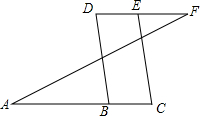 如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=
如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=