题目内容
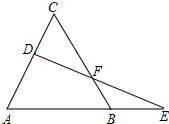 如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.
如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.(1)求证:DF=EF;
(2)若△ABC的边长为m,BE=n,且m、n满足(m-5)2=4(n-1)-n2,求BF的长.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)过D作DG∥AB,交BC于点G,可证明△CDG为等边三角形,可得CD=DG,再证明△BEF≌△GDF,即可得到DF=EF;
(2)由条件结合非负数的性质可求得m、n的值,再结合(1)可求得CG=DG=BE=2,可求得BG,则可求得BF.
(2)由条件结合非负数的性质可求得m、n的值,再结合(1)可求得CG=DG=BE=2,可求得BG,则可求得BF.
解答:
(1)证明:
如图,过D作DG∥AB,交BC于点G,
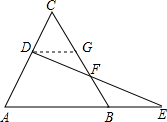
∵△ABC是等边三角形,
∴∠CDG=∠A=60°,∠CGD=∠CBA=60°,
∴△CDG为等边三角形,
∴DG=CD,
又BE=CD,
∴BE=GD,
又DG∥AB,
∴∠E=∠GDF,
在△BEF和△GDF中
∴△BEF≌△GDF(AAS),
∴DF=EF;
(2)解:
∵(m-5)2=4(n-1)-n2,
∴(m-5)2+(n-2)2=0,
∴m=5,n=2,
∴BE=DG=CG=2,BC=5,
∴BG=BC-CG=5-2=3,
又BF=FG,
∴BF=
BG=1.5.
如图,过D作DG∥AB,交BC于点G,

∵△ABC是等边三角形,
∴∠CDG=∠A=60°,∠CGD=∠CBA=60°,
∴△CDG为等边三角形,
∴DG=CD,
又BE=CD,
∴BE=GD,
又DG∥AB,
∴∠E=∠GDF,
在△BEF和△GDF中
|
∴△BEF≌△GDF(AAS),
∴DF=EF;
(2)解:
∵(m-5)2=4(n-1)-n2,
∴(m-5)2+(n-2)2=0,
∴m=5,n=2,
∴BE=DG=CG=2,BC=5,
∴BG=BC-CG=5-2=3,
又BF=FG,
∴BF=
| 1 |
| 2 |
点评:本题主要考查全等三角形的判定和性质及等边三角形的性质,掌握全等三角形的判定方法(SSS、SAS、ASA、AAS和HL)和性质(全等三角形的对应边、对应角相等)是解题的关键,在(2)中利用非负数的性质求得m、n的值是解题的关键.

练习册系列答案
相关题目
 如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )
如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )| A、24 | ||
| B、48 | ||
C、25
| ||
D、50
|
 已知,在△ABC中,∠BAC=135°,AD⊥BC,AD=2,BD=3,求DC的长.
已知,在△ABC中,∠BAC=135°,AD⊥BC,AD=2,BD=3,求DC的长.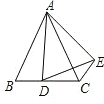 在△ABC中,AB=AC,点D是直线BC上一点(不与点B、C重合)以AD为一边,在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
在△ABC中,AB=AC,点D是直线BC上一点(不与点B、C重合)以AD为一边,在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.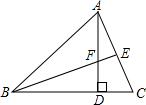 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD=BD.
如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD=BD.