题目内容
 在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,证明:BE2+CF2=EF2.
在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,证明:BE2+CF2=EF2.考点:全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理
专题:证明题
分析:延长FD到点G,使DG=DF,连接BG,易证EF=EG,△CDF≌△BDG,可得BG=CF,∠DBG=∠C,即可求得∠ABG=90°,即可判定△BEG是直角三角形,根据勾股定理可得BE2+BG2=EG2,即可解题.
解答:
 证明:延长FD到点G,使DG=DF,连接BG,
证明:延长FD到点G,使DG=DF,连接BG,
∵∠EDF=90°,DF=DG,
∴DE垂直平分FG,
∴EF=EG,
∵D是BC中点,
∴AD=BD,
在△CDF和△BDG中,
∵
,
∴△CDF≌△BDG(SAS),
∴BG=CF,∠DBG=∠C,
∵∠A=90°,
∴∠C+∠ABC=90°,
∴∠ABG=∠ABC+∠DBG=90°,
∴△BEG是直角三角形,
∴BE2+BG2=EG2,
∴BE2+CF2=EF2.
 证明:延长FD到点G,使DG=DF,连接BG,
证明:延长FD到点G,使DG=DF,连接BG,∵∠EDF=90°,DF=DG,
∴DE垂直平分FG,
∴EF=EG,
∵D是BC中点,
∴AD=BD,
在△CDF和△BDG中,
∵
|
∴△CDF≌△BDG(SAS),
∴BG=CF,∠DBG=∠C,
∵∠A=90°,
∴∠C+∠ABC=90°,
∴∠ABG=∠ABC+∠DBG=90°,
∴△BEG是直角三角形,
∴BE2+BG2=EG2,
∴BE2+CF2=EF2.
点评:本题考查了全等三角形的判定,全等三角形对应边相等的性质以及直角三角形中勾股定理的运用,本题中求证△CDF≌△BDG是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
下列命题中,真命题是( )
| A、如果x2=4,那么x=2 |
| B、对顶角相等 |
| C、相等的角是对顶角 |
| D、同旁内角互补 |
 已知,在△ABC中,∠BAC=135°,AD⊥BC,AD=2,BD=3,求DC的长.
已知,在△ABC中,∠BAC=135°,AD⊥BC,AD=2,BD=3,求DC的长.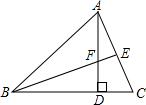 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD=BD.
如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD=BD. 如图,在△ABC中,∠B=46°,D是边BC上的一点,∠BAD=21°,DC=AB,∠CDE=46°,DE=BD,连接CE.
如图,在△ABC中,∠B=46°,D是边BC上的一点,∠BAD=21°,DC=AB,∠CDE=46°,DE=BD,连接CE.
 如图,直线AB∥x轴,与抛物线y=ax2+bx+c交于点A(-2,-
如图,直线AB∥x轴,与抛物线y=ax2+bx+c交于点A(-2,-