题目内容
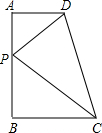如图所示，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AD=2，AB=6，BC=6，点P是AB上一个动点，则PC+PD的最小值为考点：轴对称-最短路线问题
专题：
分析：要求PC+PD的和的最小值，PC，PD不能直接求，可考虑通过作辅助线转化PC，PD的值，从而找出其最小值求解．
解答：
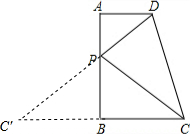1解：延长CB到C′，使C′B=CB=6，连接DC′交AB于P．则DC′就是PC+PD的和的最小值．
∵AD∥BC，
∴∠A=∠PBC′，∠ADP=∠C′，
∴△ADP∽△BC′P，
∴AP：BP=AD：BC′=2：6=1：3，
∴PB=3AP，
∵AP+BP=AB=6，
∴AP=
，BP=
，
∴PD=
=
，PC′=
=
，
∴DC′=PD+PC′=
+
=10，
∴PC+PD的最小值是10，
故答案为10．
1解：延长CB到C′，使C′B=CB=6，连接DC′交AB于P．则DC′就是PC+PD的和的最小值．∵AD∥BC，
∴∠A=∠PBC′，∠ADP=∠C′，
∴△ADP∽△BC′P，
∴AP：BP=AD：BC′=2：6=1：3，
∴PB=3AP，
∵AP+BP=AB=6，
∴AP=
| 3 |
| 2 |
| 9 |
| 2 |
∴PD=
| AD2+AP2 |
| 5 |
| 2 |
| PB2+BC′2 |
| 15 |
| 2 |
∴DC′=PD+PC′=
| 5 |
| 2 |
| 15 |
| 2 |
∴PC+PD的最小值是10，
故答案为10．
点评：此题考查了轴对称的性质、勾股定理的运用及相似三角形的判定和性质，解题时要注意找到对称点，并根据“两点之间线段最短”确定P点的位置．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况，从中抽取了一部分同学进行了一次抽样调查，利用所得数据绘制成下面的统计图：根据图中所给信息，全校喜欢娱乐类节目的学生大约有（ ）人．
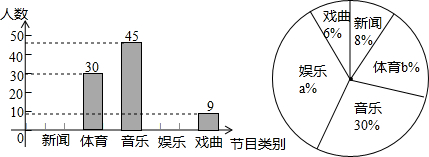
| A、1080 | B、900 |
| C、600 | D、108 |
分式
可变形为（ ）
| a |
| -a-b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
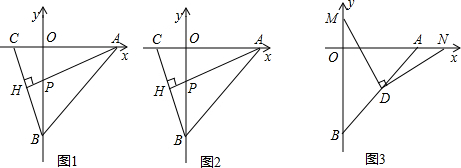
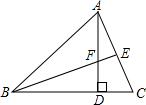如图，在△ABC中，AD⊥BC于点D，BE⊥AC于点E，AD=BD．