题目内容
10.若ab>0,ac<0,则关于x的一元二次方程ax2+bx+c=0的根的叙述正确的是( )| A. | 方程没有实数根 | |
| B. | 方程有两个不相等的正实数根或有两个不相等的负实数根 | |
| C. | 方程有一个正实数根和一个负实数根,且正实数根的绝对值较大 | |
| D. | 方程有一个正实数根和一个负实数根,且负实数根的绝对值较大 |
分析 根据ab>0、ac<0结合根的判别式即可得出△=b2-4ac>0,由此得出方程有两个不相等的实数根,再根据ab>0、ac<0即可得出$\frac{c}{a}$<0、-$\frac{b}{a}$<0,再根据根与系数的关系即可得出方程有一个正实数根和一个负实数根,且负实数根的绝对值较大.
解答 解:在方程ax2+bx+c=0中,△=b2-4ac.
∵ab>0,ac<0,
∴b2>0,-4ac>0,
∴△=b2-4ac>0,
∴方程有两个不相等的实数根.
∵ab>0,ac<0,
∴a≠0,$\frac{c}{a}$<0,-$\frac{b}{a}$<0,
∴方程有一个正实数根和一个负实数根,且负实数根的绝对值较大.
故选D.
点评 本题考查了根的判别式以及根与系数的关系,根据ab>0、ac<0找出△=b2-4ac>0和$\frac{c}{a}$<0、-$\frac{b}{a}$<0是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )| A. | sinA=$\frac{BD}{BC}$ | B. | cosA=$\frac{AC}{AD}$ | C. | tanA=$\frac{CD}{AB}$ | D. | cosB=$\frac{AC}{AB}$ |
18.某景点的门票价格如下表:
某校八年级(一)、(二)两班共102人去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元,则一共支付1118元,如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
| 购票人数 | 1~50 | 51~100 | 100以上 |
| 每人门票价 | 12 | 10 | 8 |
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
5. 已知,a,b两数在数轴上的位置如图,下列各式成立的是( )
已知,a,b两数在数轴上的位置如图,下列各式成立的是( )
 已知,a,b两数在数轴上的位置如图,下列各式成立的是( )
已知,a,b两数在数轴上的位置如图,下列各式成立的是( )| A. | ab>0 | B. | (a+1)(b+1)>0 | C. | a+b>0 | D. | (a-1)(b-1)>0 |
15.方程x(x-1)=6的解是( )
| A. | x=-2 | B. | x=3 | C. | x1=-2,x2=3 | D. | x1=2,x2=-3 |
2.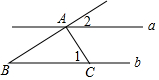 如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )
如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )
 如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )
如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )| A. | 30° | B. | 35° | C. | 45° | D. | 50° |
8.下列说法中,正确的是( )
| A. | 任意两个矩形形状相同 | B. | 任意两个菱形形状相同 | ||
| C. | 任意两个直角三角形相似 | D. | 任意两个正五边形形状相同 |
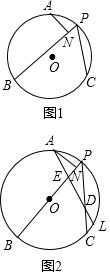 在⊙O中,PB、PC为⊙O的弦,点A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,过点A作AN⊥PB于点N,
在⊙O中,PB、PC为⊙O的弦,点A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,过点A作AN⊥PB于点N,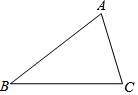 如图,在△ABC中,∠A=60°,AB=4,BC=$\sqrt{21}$,求△ABC的面积.
如图,在△ABC中,∠A=60°,AB=4,BC=$\sqrt{21}$,求△ABC的面积.