题目内容
2.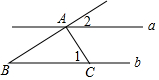 如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )
如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )| A. | 30° | B. | 35° | C. | 45° | D. | 50° |
分析 先由平行线的性质求出∠3的度数,再由余角的定义即可得出结论.
解答  解:∵直线a∥b,∠1=60°,
解:∵直线a∥b,∠1=60°,
∴∠3=∠1=60°.
∵AC⊥AB,
∴∠BAC=90°,
∴∠2=90°-∠3=90°-60°=30°.
故选A.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
10.若ab>0,ac<0,则关于x的一元二次方程ax2+bx+c=0的根的叙述正确的是( )
| A. | 方程没有实数根 | |
| B. | 方程有两个不相等的正实数根或有两个不相等的负实数根 | |
| C. | 方程有一个正实数根和一个负实数根,且正实数根的绝对值较大 | |
| D. | 方程有一个正实数根和一个负实数根,且负实数根的绝对值较大 |
17.在|-2|,-2,(-2)5,-|-2|这五个数中,负数共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
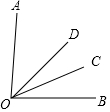 如图,OD是∠AOB的平分线,∠AOC=3∠BOC,∠COD=21°.
如图,OD是∠AOB的平分线,∠AOC=3∠BOC,∠COD=21°.