题目内容
12.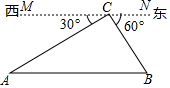 由干早年铁路建设技术不发达,只能从A地先到C地,再到B地,由于现在技术的提升,可以建设一条直接从A地到B地的公路,A,B,C三地位置关系如图所示,MN∥AB,AC=6km,BC=2$\sqrt{3}$km,
由干早年铁路建设技术不发达,只能从A地先到C地,再到B地,由于现在技术的提升,可以建设一条直接从A地到B地的公路,A,B,C三地位置关系如图所示,MN∥AB,AC=6km,BC=2$\sqrt{3}$km,(1)用方向角和实际距离分别表示A地,B地相对于C地的位置;
(2)若以A地为原点建立平面直角坐标系,且AC=6,点B在x轴上,求B地的坐标.
分析 (1)根据方向角定义可得;
(2)根据余弦函数的定义即可得.
解答 解:(1)由题意知A地在C地西偏南30°方向,距离C地6km位置,
B地在C地东偏南60°方向,距离C地2$\sqrt{3}$km位置;
(2)如图,由题意知,∠ACB=90°,
∵MN∥BC,
∴∠CAB=30°,
则AB=$\frac{AC}{cos∠CAB}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$,
∴点B的坐标为(4$\sqrt{3}$,0).
点评 本题主要考查解直角三角形的应用,熟练掌握方向角和余弦函数的定义是解题的关键.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | (-5)0=0 | B. | x2+x3=x5 | C. | 2a2•a-1=2a | D. | (ab2)3=a2b5 |
3.使代数式$\frac{2x}{x-2}$有意义的x的取值范围为( )
| A. | x>2 | B. | x≠0 | C. | x<2 | D. | x≠2 |
1.抛物线y=2(x+3)2-2的顶点坐标是( )
| A. | (-3,2) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
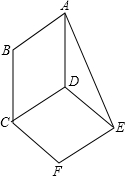 如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠DAE=25°,则∠F的度数为110°.
如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠DAE=25°,则∠F的度数为110°.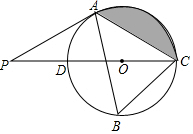 如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.
如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.