题目内容
4.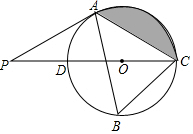 如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.
如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.(1)求∠ACP的度数;
(2)求PD的长;
(3)求阴影部分的面积S.
分析 (1)在Rt△ADC中,求出∠ADC即可解决问题.
(2)首先证明PA=AC,在Rt△PAO中,根据AO=PA•tan30°=$\frac{5\sqrt{3}}{3}$,OP=2OA=$\frac{10\sqrt{3}}{3}$即可解决问题.
(3)根据S阴=S扇形OAC-S△AOC计算即可.
解答 解:(1)如图连结OA、AD.
∵CD是⊙O的直径,
∴∠DAC=90°,
∵∠ADC=∠B=60°,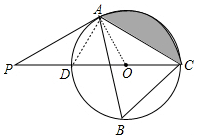
∴∠ACP=30°,
(2)∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵∠AOD=2∠ACD=60°,
∴∠P=90°-60°=30°,
∴∠P=∠ACP,
∴AP=AC=5,
在Rt△PAO中,AO=PA•tan30°=$\frac{5\sqrt{3}}{3}$,OP=2OA=$\frac{10\sqrt{3}}{3}$,
∴PD=OP=OD=$\frac{5\sqrt{3}}{3}$.
(3)S阴=S扇形OAC-S△AOC=$\frac{120•π•(\frac{5\sqrt{3}}{3})^{2}}{360}$-$\frac{1}{2}$•5•$\frac{5\sqrt{3}}{6}$=$\frac{25π}{9}$-$\frac{25\sqrt{3}}{12}$.
点评 本题考查切线的性质、圆周角定理、扇形的面积公式、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
15.已知a+b+c=0,则$\frac{\sqrt{{a}^{2}}}{a}+\frac{\sqrt{{b}^{2}}}{b}+\frac{\sqrt{{c}^{2}}}{c}$的值可能是1或-1.
9. 如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:
如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:
①a<0,②b<0,③b2-4ac>0,④AE+CD=4
下列选项中选出的结论完全正确的是( )
 如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:
如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:①a<0,②b<0,③b2-4ac>0,④AE+CD=4
下列选项中选出的结论完全正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①② |
7.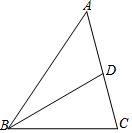 如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
 如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
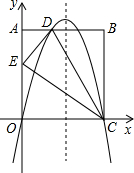 如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.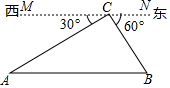 由干早年铁路建设技术不发达,只能从A地先到C地,再到B地,由于现在技术的提升,可以建设一条直接从A地到B地的公路,A,B,C三地位置关系如图所示,MN∥AB,AC=6km,BC=2$\sqrt{3}$km,
由干早年铁路建设技术不发达,只能从A地先到C地,再到B地,由于现在技术的提升,可以建设一条直接从A地到B地的公路,A,B,C三地位置关系如图所示,MN∥AB,AC=6km,BC=2$\sqrt{3}$km,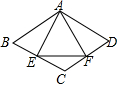 如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,下列结论:①AE=AF;②∠EAF=60°;③△CEF是等腰三角形;④AF=$\sqrt{3}$cm,其中结论正确的个数是( )
如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,下列结论:①AE=AF;②∠EAF=60°;③△CEF是等腰三角形;④AF=$\sqrt{3}$cm,其中结论正确的个数是( )