题目内容
20．若点（x1，y1），（x2，y2），（x3，y3）都是反比例函数y=-$\frac{1}{x}$图象上的点，并且y1＜0＜y2＜y3，则x1，x2，x3的大小关系是x2＜x3＜x1．分析 先根据反比例函数的解析式判断出函数图象所在的象限及其增减性，再由y1＜0＜y2＜y3判断出各点所在的象限，进而可得出结论．
解答 解：∵函数y=-$\frac{1}{x}$中，k=-1＜0，
∴此函数的图象的两个分支位于二四象限，且在每一象限内，y随x的增大而增大．
∵y1＜0＜y2＜y3，
∴点（x1，y1）在第四象限，（x2，y2）、（x3，y3）在第二象限，
∴x1＞0，x2＜x3＜0，
∴x2＜x3＜x1．
故答案为：x2＜x3＜x1．
点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
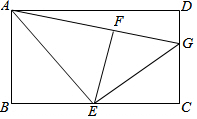如图，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G．
15．已知a+b+c=0，则$\frac{\sqrt{{a}^{2}}}{a}+\frac{\sqrt{{b}^{2}}}{b}+\frac{\sqrt{{c}^{2}}}{c}$的值可能是1或-1．
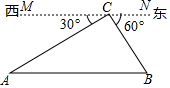由干早年铁路建设技术不发达，只能从A地先到C地，再到B地，由于现在技术的提升，可以建设一条直接从A地到B地的公路，A，B，C三地位置关系如图所示，MN∥AB，AC=6km，BC=2$\sqrt{3}$km，
如图抛物线y=ax2+bx+c与x轴交于A、B两点，其中B点坐标为（4，0），直线DE是抛物线的对称轴，且与x轴交于点E，CD⊥DE于D，现有下列结论：