题目内容
17．
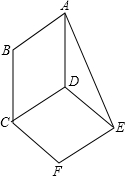如图，?ABCD与?DCFE的周长相等，且∠BAD=60°，∠DAE=25°，则∠F的度数为110°．
分析 由，?ABCD与?DCFE的周长相等，可得到AD=DE即△ADE是等腰三角形，再由且∠BAD=60°，∠DAE=25°，即可求出∠F的度数．
解答 解：∵?ABCD与?DCFE的周长相等，且CD=CD，
∴AD=DE，
∴∠DAE=∠DEA=25°，
∴∠ADE=130°，
∵∠BAD=60°，
∴∠ADC=120°，
∴∠CDE═∠F=360°-130°-120°=110°．
故答案为：110°．
点评 本题考查了平行四边形的性质：平行四边形的对边相等、平行四边形的对角相等以及邻角互补和等腰三角形的判定和性质、三角形的内角和定理，得出∠ADE的度数是解题关键．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
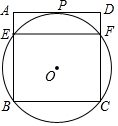如图，过正方形ABCD顶点B，C的⊙O与AD相切于点P，与AB，CD分别相交于点E，F，连接EF．
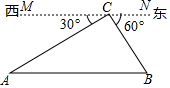由干早年铁路建设技术不发达，只能从A地先到C地，再到B地，由于现在技术的提升，可以建设一条直接从A地到B地的公路，A，B，C三地位置关系如图所示，MN∥AB，AC=6km，BC=2$\sqrt{3}$km，
如图抛物线y=ax2+bx+c与x轴交于A、B两点，其中B点坐标为（4，0），直线DE是抛物线的对称轴，且与x轴交于点E，CD⊥DE于D，现有下列结论：