题目内容
7. 如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)
如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)
分析 仔细观察图形与序列数之间的关系,分别确定第n个图形中“●”和“△”的个数,从而确定答案.
解答 解:∵观察图象得:第1个图形中有“●”4×1个、“△”4=22个;
第2个图形中有“●”4×2个、“△”32个
第1个图形中有“●”4×3个、“△”42个
…
∴第n个图形中有“●”4n个、“△”(n+1)2个,
∴第n个图案中“●”和“△”的个数之和为(n+1)2+4n个“●”和“△”,
故答案为:(n+1)2+4n.
点评 本题考查了图形的变化类问题,解题的关键是分别确定“●”和“△”的个数,难度不大.

练习册系列答案
相关题目
18.某村准备在坡度(坡面的铅直高度与水平宽度之比)为$\frac{1}{3}$的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离为( )米.
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$$\sqrt{10}$ | D. | $\sqrt{10}$ |
2.某班统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如下表,则这10名同学在一周内累计时间的众数是( )
| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
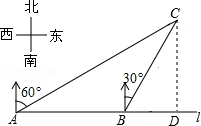 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km.
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km. 某市园林局准备种植A种花木4200棵,B种花木2400棵.现计划安排26人同时种植这两种花木,已知每人每天能种植A种花木30棵或B种花木20棵,则应分别安排多少人种植这两种花木,才能确保同时完成各自的任务?
某市园林局准备种植A种花木4200棵,B种花木2400棵.现计划安排26人同时种植这两种花木,已知每人每天能种植A种花木30棵或B种花木20棵,则应分别安排多少人种植这两种花木,才能确保同时完成各自的任务?