题目内容
3.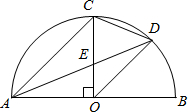 如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )| A. | AC∥OD | B. | CD2=CE•CO | C. | S△AEC=2S△DOE | D. | AC=2CD |
分析 根据等腰三角形的性质和角平分线的性质,利用等量代换求证∠CAD=∠ADO即可得到A正确,过点O作OG⊥AC,再根据直角三角形斜边大于直角边可证D错误;利用相似三角形的判定与性质以及等腰直角三角形的性质得出即可C正确;根据相似三角形的性质即可得到B正确.
解答 证明:∵AB是半圆直径,
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=$\frac{1}{2}$∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∴故A选项正确.
如图1,过点O作OG⊥AC,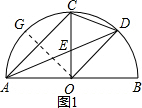 ∵OG⊥AC,
∵OG⊥AC,
∴$\widehat{AG}=\widehat{CG}$,
∵半径OC⊥AB于点O,
∴$\widehat{AG}$=$\widehat{CG}$=$\widehat{CD}$,
∴AG=GC=CD,
∴AC<2CD,
∴故D选项错误.
如图2,过点E作EM⊥AC于点M,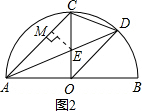 ∵AO=CO,AO⊥CO,
∵AO=CO,AO⊥CO,
∴∠CAO=∠ACO=45°,
∴CM=ME,
∵AD平分∠CAB分别交OC于点E,
EO⊥AO,EM⊥AC,
∴ME=EO,
∴CM=ME=EO,
∴CE=$\sqrt{2}$ME=$\sqrt{2}$EO,
由①得:∵AC∥OD,
∴△ACE∽△DOE,
∴$\frac{EC}{EO}$=$\sqrt{2}$,
∴$\frac{{S}_{△AEC}}{{S}_{△DEO}}$=($\sqrt{2}$)2=2,
∴S△AEC=2S△DEO;故C正确,
∵OC⊥AB,OA=OC,
∴△AOC为等腰直角三角形,
∴∠DOB=∠COD=∠BAC=45°,
∵∠ADC与∠AOC都对$\widehat{AC}$,
∴∠ADC=$\frac{1}{2}$∠AOC=45°,
∴∠ADC=∠COD,又∠OCD=∠DCE,
∴△DCE∽△OCD,
∴$\frac{DC}{OC}=\frac{CE}{CD}$,即CD2=CE•OC,
故B正确.
故选D.
点评 此题考查了圆周角定理,圆心角、弧及弦之间的关系,以及相似三角形的判定与性质,熟练掌握圆周角定理是解本题的关键.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$$\sqrt{10}$ | D. | $\sqrt{10}$ |
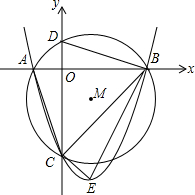 如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为$\sqrt{5}$,设⊙M与y轴交于D,抛物线的顶点为E.
如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为$\sqrt{5}$,设⊙M与y轴交于D,抛物线的顶点为E.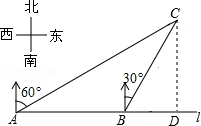 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km.
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km. 某市园林局准备种植A种花木4200棵,B种花木2400棵.现计划安排26人同时种植这两种花木,已知每人每天能种植A种花木30棵或B种花木20棵,则应分别安排多少人种植这两种花木,才能确保同时完成各自的任务?
某市园林局准备种植A种花木4200棵,B种花木2400棵.现计划安排26人同时种植这两种花木,已知每人每天能种植A种花木30棵或B种花木20棵,则应分别安排多少人种植这两种花木,才能确保同时完成各自的任务?