题目内容
6.已知有理数a,b,c满足|a-c-2|+|3a-6b-7|+(3b+3c-4)2=0,则abc=1.分析 利用非负数的性质:几个非负数的和等于0,则每个数等于0,即可列方程组求得a、b、c的值,进而求得代数式的值.
解答 解:根据题意得:$\left\{\begin{array}{l}{a-c-2=0}\\{3a-6b-7=0}\\{3b+3c-4=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=3}\\{b=\frac{1}{3}}\\{c=1}\end{array}\right.$,
则abc=1.
故答案是:1.
点评 本题考查二元一次方程组的解法,解方程组的基本思想是消元、消元的方法有代入消元法和加减消元法两种.

练习册系列答案
相关题目
 根据要求画图:
根据要求画图: 如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结 CD、EB.
如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结 CD、EB. 如图,半圆O绕点M旋转,点O旋转到点O′,画出半圆O绕点M旋转后得到的图形.
如图,半圆O绕点M旋转,点O旋转到点O′,画出半圆O绕点M旋转后得到的图形.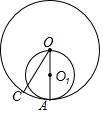 已知:如图,⊙O的半径OA为⊙O1的直径,⊙O的半径OC交⊙O1于点B,求证:$\widehat{AB}$的长等于$\widehat{AC}$的长.
已知:如图,⊙O的半径OA为⊙O1的直径,⊙O的半径OC交⊙O1于点B,求证:$\widehat{AB}$的长等于$\widehat{AC}$的长.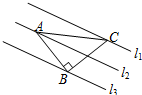 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是$\sqrt{26}$.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是$\sqrt{26}$.