题目内容
15.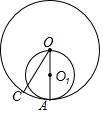 已知:如图,⊙O的半径OA为⊙O1的直径,⊙O的半径OC交⊙O1于点B,求证:$\widehat{AB}$的长等于$\widehat{AC}$的长.
已知:如图,⊙O的半径OA为⊙O1的直径,⊙O的半径OC交⊙O1于点B,求证:$\widehat{AB}$的长等于$\widehat{AC}$的长.
分析 根据圆周角定理可得出∠AO1B=2∠AOB,设∠AOB=θ,则∠AO1B=2θ,再根据弧长公式可得出结论.
解答  解:设∠AOB=θ,⊙O1的半径O1A=r,则OA=2r,∠AO1B=2∠AOB=2θ,
解:设∠AOB=θ,⊙O1的半径O1A=r,则OA=2r,∠AO1B=2∠AOB=2θ,
∵$\widehat{AC}$的长度=$\frac{θπ•2r}{180}$=$\frac{θπr}{90}$,
$\widehat{AB}$的长度=$\frac{2θπ•r}{180}$=$\frac{θπr}{90}$,
∴两弧的长度相等.
即:$\widehat{AB}$的长等于$\widehat{AC}$的长.
点评 本题考查了弧长的计算以及圆周角定理,熟记弧长的公式是解此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
4.已知关于x不等式2x2+bx-c>0的解集为{x|x<-1或x>3},则关于x的不等式bx2+cx+4≥0的解集为( )
| A. | {x|x≤-2或x≥$\frac{1}{2}$} | B. | {x|x≤-$\frac{1}{2}$或x≥2} | C. | {x|-$\frac{1}{2}$≤x≤2} | D. | {x|-2≤x≤$\frac{1}{2}$} |
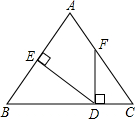 如图,△ABC中,∠A=∠B,FD⊥BC,DE⊥AB,垂足分别为D、E,∠AFD=160°.
如图,△ABC中,∠A=∠B,FD⊥BC,DE⊥AB,垂足分别为D、E,∠AFD=160°.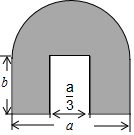 如图是一个工件的横断面及其尺寸.(单位:cm).
如图是一个工件的横断面及其尺寸.(单位:cm). 已知:如图,AD=AC,∠1=∠2,∠B=∠E.求证:BC=ED.
已知:如图,AD=AC,∠1=∠2,∠B=∠E.求证:BC=ED.