题目内容
12．下列计算正确的是（ ）| A． | a3÷a2=a | B． | （-2a2）3=8a6 | C． | 2a2+a2=3a4 | D． | （a-b）2=a2-b2 |
分析 根据同底数幂的除法底数不变指数相减，积的乘方等于乘方的积，合并同类项系数相加字母及指数不变，差的平方等于平方和减积的二倍，可得答案．
解答 解：A、同底数幂的除法底数不变指数相减，故A正确；
B、积的乘方等于乘方的积，故B错误；
C、合并同类项系数相加字母及指数不变，故C错误；
D、差的平方等于平方和减积的二倍，故D错误；
故选：A．
点评 本题考查了同底数幂的除法，熟记法则并根据法则计算是解题关键．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
20．
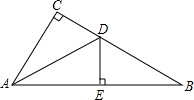如图，在直角三角形ABC中，∠C=90°，∠CAB的平分线ADD交BC于点D，若DE垂直平分AB，则下列结论中错误的是（ ）
如图，在直角三角形ABC中，∠C=90°，∠CAB的平分线ADD交BC于点D，若DE垂直平分AB，则下列结论中错误的是（ ）| A． | AB=2AE | B． | AC=2CD | C． | DB=2CD | D． | AD=2DE |
17．抛物线y=-4x2+5的开口方向（ ）
| A． | 向上 | B． | 向下 | C． | 向左 | D． | 向右 |
1．在Rt△ABC中，∠ACB=90°，BC=1，AB=2，则下列结论正确的是（ ）
| A． | $sinA=\frac{{\sqrt{3}}}{2}$ | B． | $cosA=\frac{{\sqrt{3}}}{2}$ | C． | $tanA=\frac{1}{2}$ | D． | $cotA=\frac{{\sqrt{3}}}{3}$ |
2．在?ABCD中，AB≠CD，满足下列条件，不一定能构成平行四边形的是（ ）
| A． | 四个内角平分线围成的四边形 | |
| B． | 过四个顶点作对边的高线围成的四边形 | |
| C． | 以各边中点为顶点的四边形 | |
| D． | 以一条对角线上的两点与另两个顶点为顶点的四边形 |