题目内容
5.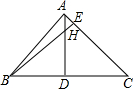 如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由.
如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由.
分析 (2)求出∠DBH=∠DAC,根据ASA证△BDH≌△ADC,根据全等三角形的性质推出即可;
解答 解:结论:BH=AC.
理由:∵AD,BE是△ABC的高
∴∠ADC=∠BEC=90°,
∴∠DBH+∠C=90°,∠DAC+∠C=90°
∴∠DBH=∠DAC;
在△BDH和△ADC中,
$\left\{\begin{array}{l}{∠BDH=∠ADC}\\{BD=AD}\\{∠DBH=∠DAC}\end{array}\right.$,
∴△BDH≌△ADC(ASA),
∴BH=AC;
点评 此题主要考查了全等三角形的判定与性质,解决此题的关键是根据同角的余角相等证明∠CBE=∠CAD.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
19.一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是( )
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐60°,第二次右拐60° | ||
| C. | 第一次左拐60°,第二次左拐120° | D. | 第一次右拐60°,第二次右拐60° |
20. 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )
 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )| A. | 4 | B. | $\sqrt{15}$ | C. | $\sqrt{7}$ | D. | $\sqrt{6}$ |
 已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.
已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.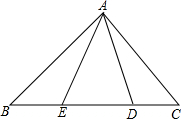 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).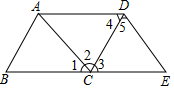 如图,点E在BC的延长线上,下列条件中,
如图,点E在BC的延长线上,下列条件中, 如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.
如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.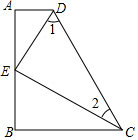 如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由.
如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由.