题目内容
16. 已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.
已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.
分析 根据已知条件和全等三角形的判定条件证出△DEB≌△DFC,由全等三角形的性质得出∠B=∠C,最后根据等角对等边即可得出答案.
解答 解:∵DE⊥AB,DF⊥AC,
∴∠DEB=90°,∠DFC=90°,
∵AD是∠BAC的角平分线,
∴DE=DF,
在△DEB和△DFC中,
$\left\{\begin{array}{l}{DE=DF}\\{BD=CD}\end{array}\right.$,
∴△DEB≌△DFC(HL),
∴∠B=∠C,
∴AB=AC.
点评 此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质、等腰三角形的判定以及角平分线的性质,关键是证出△DEB≌△DFC,此题难度不大,属于基础题.

练习册系列答案
相关题目
10.若(x3)m=x9,则m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.将点A(-1,2)向右平移4个单位长度,再向下平移3个单位长度,则平移后点的坐标是( )
| A. | (3,1) | B. | (-3,-1) | C. | (3,-1) | D. | (-3,1) |
11.若x=-3是方程kx-x+6=0的解,则k的值是( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
 如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.
如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.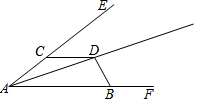 如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC).
如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC).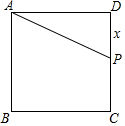 如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.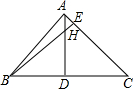 如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由.
如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由.